Partie 5.
Objets composés, Vecteurs
COURS 13 : les objets composés
COURS 14 : Vecteur
COURS 15: Algorithmes sur les vecteurs
COURS 16: Vecteur de vecteur
Partie 5
Objets composés
COURS 13 : les objets
composés ![]()
13.1 Introduction
La mémoire est une suite finie de mots ( de longueur 16 bits pour les micro-ordinateurs ) adressée de 0 à N ( N dépend de la machine).
A chaque objet ( variable / constante) est associée une représentation : entier, réel, booléen, caractère...
A chaque mode de représentation est associé un ensemble d'opérations. Ainsi, on distingue le + entier du + réel, etc.
Le langage algorithmique est un outil de description puissant. De la même façon que l'on peut construire des actions composées et de les utiliser en tant que telles au niveaux des corps d'algorithmes on peut aussi définir des objets complexes appartenant à un autre type que l'on décrit au niveau de l’en-tête.
13.2 Définition de type
Au niveau du langage algorithmique un type est construit comme suit :
TYPE Nomdutype = Structure |
Typei peut être un type standard ou construit.
Exemple
Type article = Structure
Nom : car
Prenom : car
Age : entier
Fin
13.3 Déclaration des variables
On peut maintenant définir des objets de type article comme suit:
Var X : article
On peut aussi si nécessaire définir une relation d'ordre entre les éléments appartenant à une même classe d'objets.
13.4 Accès
Si X est une variable de type article, X.Nom permet d’accéder au champ Nom de la variable composée X.
Noter l'imbrication de type ( arborescence )
13.5 Utilisation en Pascal
Un type ou classe d'objet est défini par
| TYPE nom du type = RECORD Nom1 : type1 ; Nom2 : type2 ; .... Nomp : typep END |
Les variables de cette classe sont définies par :
| VAR N1, N2, ..... : nom du type |
L'accès se fait par le chemin et utilisation des points
| N1.M1.P1........... |
COURS 14 : Vecteur
![]()
14.2 Caractéristiques
Considérons l’exemple du dictionnaire :
Si l'on veut chercher un élément dans un dictionnaire, on n'est pas obligé de parcourir toutes les pages précédentes. On dira que l'accès à un élément du dictionnaire est direct.
En général, l'élément recherché ( définition ) est caractérisé par son indicatif.
Les mots sont ordonnées. On ouvre le dictionnaire au hasard et au vu des mots, soit on recherche dans les pages antérieures ou dans les pages postérieures.
On peut aussi parcourir un dictionnaire du début vers la fin, c'est l'accès séquentiel.
En informatique certains dispositifs physiques de stockage possèdent cette propriété d'accès direct. On peut citer comme exemples les mémoires centrales des ordinateurs et les disques.
14.3 Définition formelle Soient- V, un ensemble fini quelconque d'éléments : l'ensemble des valeurs.
- N, un entier, nombre d'éléments du vecteur.
Un vecteur peut être défini comme une application d'un intervalle I de N formé de n éléments de V.
I est appelé l'ensemble des index ( indices ).
Remarques
- L'ensemble des indices est noté [ 1, N ]
- Un vecteur peut être vide
- On peut définir un vecteur par son graphe, c’est à dire l’ensemble des couples (indice, valeur)
- Un élément peut être : simple, structuré, ou même un autre vecteur.
- On peut définir une relation d'ordre dans l'ensemble des valeurs.
14.4 Terminologie et NotationDéfinissons quelques termes sur les vecteurs.
Borne inférieure :
C’est le plus petit élément de l’ensemble des indices.
Borne supérieure
C’est le plus grand élément de l’ensemble des indices.
Taille
C’est le nombre d'élément du vecteur.
Notation
Un vecteur est noté ( T[1,n], V)
Un élément est le couple ( i, T(i) ) ou T(i)
Sous vecteur
C’est la restriction de T à un intervalle de l’ensemble des indices.
14.5 Accès à un élément du vecteurIl n'existe qu'une opération d'accès : l'opération d'indexation.
Soit un vecteur T[1:N]
quelque soit i dans [1, n] : T(i) délivre la valeur de l’élément d'indice i dans le vecteur T.
Si i n'est pas dans [1, n], T(i) est indéfini.
Remarque
- T(1) donne l'accès au premier élément.
- On peut faire les affectations := T(i) ou T(i) := a
14.6 Vecteur ordonnéOn parle d’un vecteur ordonné quand l'ensemble des valeurs possibles est muni d'une relation d'ordre. De plus, un vecteur est dit ordonné ou trié en ordre croissant si quelque soit i dans [1, n-1] : T(i) <= T(i+1)
14.7 MesuresMesurer un algorithme sur les vecteurs consiste à déterminer son encombrement et le nombre d’affectations et comparaisons portant uniquement sur les éléments du vecteur.
On désigne par encombrement d’un vecteur le produit de sa taille par l’espace occupé par un de ses éléments.
14.8 Description algorithmiqueOn décrit un vecteur comme suit :
VAR nomdutableau : TABLEAU [1..N] DE type |
COURS 15 .
Algorithmes sur les vecteurs ![]()
15.1 Algorithmes traitant un seul vecteur
On distingue généralement deux classes d’algorithmes :
- les algorithmes de parcours en vu de réaliser un traitement donné.
- les algorithmes de parcours en vu de rechercher une valeur donnée.
Exemples
Considérons quelques algorithmes :
Recherche dichotomique dans un vecteur
On ne peut faire ce type de recherche que dans le cas où le vecteur est ordonné. Le principe est le suivant :
On utilise 3 variables : Bi, Bs et Milieu, représentant respectivement la borne inférieure, la borne supérieure et l’indice du milieu, c’est à dire (Bi + Bs) /2.
Initialement Bi est 1 et Bs et M ( taille du vecteur)
Considérons la valeur se trouvant au milieu du vecteur V[Bi ..Bs] c’est à dire V[Milieu].
Si V[Milieu] est la donnée recherchée, la recherche se termine avec succès.
Autrement, comme le vecteur est ordonné, à ce niveau on peut orienter la recherche uniquement dans l’un des deux sous vecteurs en modifiant Bi ou Bs selon que l’élément recherché est supérieur ou inférieur à V[Milieu].
L’algorithme est le suivant :
| ALGORITHME
Dichotomie VAR V : TABLEAU[1..M] DE ENTIER D, Bi, Bs, Milieu : ENTIER Trouv : BOOLEEN DEBUT LIRE(V) LIRE(D) Bi := 1 Bs := M Trouv := FAUX TANTQUE Bi <= Bs et NON Trouv Milieu := (Bi + Bs ) /2 Si V[Milieu] = D Trouv := VRAI SINON SI D < V[Milieu] Bs := Milieu - 1 SINON Bi := Milieu + 1 FSI FSI FINTANTQUE FIN |
Recherche séquentielle dans un vecteur
Il s’agit de rechercher un élément séquentièllement à partir de la première position du tableau.
| ALGORITHME
Recherche1 VAR V : TABLEAU[1..M] DE ENTIER D, I: ENTIER Trouv : BOOLEEN DEBUT LIRE(V) LIRE(D) I := 1 Trouv := FAUX TANTQUE I <= M et NON Trouv Si V[I] = D Trouv := VRAI SINON I := I + 1 FSI FINTANTQUE FIN |
Recherche séquentielle dans un vecteur ordonné
Il s’agit de rechercher un élément séquentièllement à partir de la première position du tableau. De plus, si on rencontre un élément supérieur à l’élément recherché, on arrête le parcours du vecteur.
| ALGORITHME
Recherche2 VAR V : TABLEAU[1..M] DE ENTIER D, I: ENTIER Trouv, Arret: BOOLEEN DEBUT LIRE(V) LIRE(D) I := 1 Trouv, Arret := FAUX TANTQUE I <= M et NON Trouv et NON Arret Si V[I] = D Trouv := VRAI SINON SI V[I] > D Arret := VRAI SINON I := I + 1 FSI FSI FINTANTQUE FIN |
Exemple : Interclassement de deux vecteurs
L’interclassement de deux vecteurs exigent que les vecteurs soient ordonnés. Il consiste à construire un troisième vecteur ordonné contenant tous les éléments des deux vecteurs.
L’algorithme est le suivant :
| ALGORITHME
Interclasser VAR V1 : TABLEAU[1..N1] DE ENTIER V2 : TABLEAU[1..N2] DE ENTIER V3 : TABLEAU[1..N1+N2] DE ENTIER I, J, K: ENTIER DEBUT LIRE(V1, V2) I, J:= 1 K := 0 TANTQUE I <= N1et J <= N2 K := K + 1 SI V1[I] < V2[J] V3[K] := V1[I] I := I + 1 SINON V3[K] := V2[J] J := J + 1 FSI FINTANQUE TANTQUE I <= N1 K := K + 1 V3[K] := V1[I] I := I + 1 FINTANQUE TANTQUE J <= N2 K := K + 1 V3[K] := V2[J] J := J + 1 FINTANQUE FIN |
On distingue trois type de modification :
Modification
Elle consiste à remplacer une valeur par une autre.
Insertion
Elle consiste à ajouter une autre valeur. On peut rajouter à la fin ou à n’importe quelle position du vecteur. Dans ce dernier cas, on fera des décalages.
Soit un vecteur V[1..M] contenant N éléments. L’algorithme qui suit insère la valeur D à la K-ième position
| ALGORITHME Inserer VAR V : TABLEAU[1..M] DE ENTIER D, I, K: ENTIER DEBUT LIRE(V) /* Remplir le vecteur avec N élément */ LIRE(N) /* Nombre d'éléments présents dans le vecteur */ LIRE(D) /* la donnée à insérer */ LIRE(K) /* la position où il faut insérer */ SI N < M N := N + 1 POUR I :=N, K-1 V[I+1] := V[I] FINPOUR V[K] := D SINON ECRIRE('Saturation du vecteur ') FSI FIN |
Suppression
La suppression peut être logique ou physique. Supprimer logiquement un élément consiste à utiliser un champ additionnel pour indiquer la présence ou l’abscence de l’élément . Supprimer physiquement un élément consiste à l’éliminer complètement du vecteur. On procédera donc par décalage.
15.4 Algorithmes de tri Plusieurs méthodes de tri existent. Exposons dans ce qui suit quelques unes.Tri par sélection
Tri par sélection
On utilise 2 vecteurs, soit VNT (vecteur à trier ) et VT (vecteur résultat trié). On peut énoncer l’algorithme comme suit :
| a) chercher le maximum dans VNT, soit
Max b) répéter (n-1) fois les étapes suivantes : - chercher le minimum dans VNT, soit Min - remplacer le par Max - mettre Min dans VT successivement de la position 1 à n. |
Tri part sélection et permutation
On utilisation un seul vecteur. La technique est la suivante :
| a) rechercher le maximum dans V[1..N],
soit R son rang b) permuter l'élément de rang R avec l'élément de rang N Répéter a) et b) successivement dans les sous-vecteurs V[1..N-1], V[1..N-2], ..... |
Tri par bulles
Un seul vecteur est utilisé. Le procédé est le suivant :
Par une série de permutations 2 à 2 ramener le maximum à la dernière position. Répéter cette opération successivement dans les sous-vecteurs V[1..N-1], V[1..N-2],
Formellement, l’algorithme est le suivant :
Tri par Comptage
| ALGORITHME Tribulles VAR V : TABLEAU[1..M] DE ENTIER I, J, Temp: ENTIER DEBUT LIRE(V) /* Remplir le vecteur avec N élément */ POUR I :=1, M-1 POUR J := M, I+1, -1 SI V[J-1] > V[J] Temp := V[J-1] V[J-1] := V[J] V[J] := Temp FSI FINPOUR FINPOUR FIN |
On utilise deux vecteurs : V[1..N] et COMPT[1..N]. On procédera comme suit :
| a) initialisation globale de COMPT à
1. b) prendre successivement chaque élément, soit V(i), du vecteur à trier et le comparer avec les éléments suivants V(k), k=i+1, i+2, ... Si V(i) > V(k) on incrémente COMPT(i) d'une unité sinon on incrémente COMPT(k) d'une unité |
Un vecteur V est défini en PASCAL par la déclaration
VAR V : ARRAY[Bi ..Bs] OF Typeqq |
Où Bi et Bs désignent les limites de l’intervalle des indices. Typeqq désigne un type quelconque.
L’accès au I-ème élément se fait par V[I].
Contentons nous de traduire en PASCAL l’algorithme de tri par bulles décrit précédemment.
| PROGRAM Tribulles ; CONST M = 20 ; VAR V : ARRAY [1..M] OF INTEGER ; I, J, Temp: INTEGER ; BEGIN /* Remplir le vecteur avec M éléments */ FOR I :=1 TO M DO READ(V[I] ) ; /* Tri */ FOR I :=1 TO M-1 DO FOR J := M DOWNTO I+1 DO IF V[J-1] > V[J] THEN BEGIN Temp := V[J-1] V[J-1] := V[J] V[J] := Temp END END. |
COURS 16.
Vecteur de vecteur ![]()
16.1 Vecteur de vecteurs ou matrice
Les éléments d’un vecteur peuvent être de type quelconque. On peut avoir par exemple un vecteur d’entier, un vecteur de caractères ou un vecteur d’objets composés. Les éléments d’un vecteurs peuvent aussi être des vecteurs. On parlera alors de vecteur de vecteurs ou tout simplement de matrice ou encore tableau à deux dimensions.
16.2 Vecteur à n dimensions
De même, les éléments d’une matrice peuvent être de type quelconque. On peut avoir par exemple une matrice d’entier, de caractères ou d’objets composés. Les éléments d’une matrice peuvent aussi être des vecteurs. On parlera alors de matrice de vecteurs ou tout simplement de tableau à trois dimensions.
De cette façon, on peut généraliser à l’ordre n.
16.3 Représentation mémoire
Considérons un tableau à n dimensions défini par
A(a1:b1; a2:b2; ......an:bn)
Où a1, a2,… , an désignent les bornes inférieurs dans chaque dimension et b1, b2, …., bn les bornes supérieures.
En mémoire centrale, le rangement se fait par sous tableau A(i, *, *, ..., *) pour i variant de a1 à b1 comme suit :
A(a1, *, *, ..., *),
A(a1+1, *, *, ..., *),
A(a1+2, *, *, ..., *),
.........,
A(b1, *, *, ..., *)
A l'intérieur de chaque sous tableau A(i, *, *, ...., *), l'ordre suivant des sous sous-tableaux est considéré :
A(i, a2, *, *, ..., *),
A(i, a2+1, *, *, ..., *),
......,
A(i, b2, *, *, ..., *)
Et ainsi de suite ...
Donc le rangement de la matrice ligne par ligne. De plus, ce sont les derniers indices qui varient le plus rapidement.
Exemple :
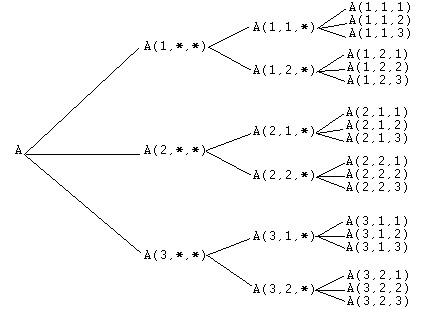
Comment déterminer l'adresse d'un élément A(i1,i2 ..,in)?
Posons di = bi - ai + 1
L’adresse de A(i1, *, *, ....) :
AD1 = Base + (i1-a1) d2d3...dn
Base étant l’adresse début du tableau.
L’adresse de A(i1, i2, *, ...., *) est
AD2 = AD1 + (i2-a2)d3d4...dn
L’adresse de A(i1, i2, ...in) est
ADn = (i1-a1)d2d3..dn + (i2-a2)d3d4...dn + ....+(in-1-an-1)dn + (in-an)
Dans cette formule, il y a une partie constante et une partie variable.
Partie constante :
Base -(a1 Õ di + a2 Õ di+..+an-1dn + an)
i=2,n i=3,n
Partie variable
I1 Õ di + i2 Õ di + ... + in-1dn + in
i=2, n i=3, n
Si a1 = a2 = ...... = an = 0, l'adresse de A(i1, i2, ...in) est
i1d2d3..dn + i2d3d4...dn + ....+in-1dn + in
Ou bien :
å ( ij . Õ di )
j=1,n i=j+1, n
1. Algorithme traitant un seul vecteur
- Recherche du maximum dans un vecteur.
- Moyenne des élèves dans une classe de n élèves pour une matière donnée.( Un élément du vecteur est une structure à 2 champs : Nom, Note ).algorithme et programme.
- Calcul d'un polynôme de degré n donné par le tableau de ses coefficients pour une valeur de x donnée.
- Admission dans une école avec baccalauréat C et moyenne supérieure ou égale à 10 ou Bac D et moyenne supérieure ou égale à 11 ou Bac B et moyenne supérieur ou égale à 13. Algorithme et Programme Pascal.
2. Algorithmes traitant plusieurs vecteurs
- Soient 2 vecteurs A[1..N] et B[1..M] d'entiers. Construire un troisième vecteur C contenant tous les éléments de A et B qui sont des carrés.
- Construire le vecteur intersection à partir deux vecteurs donnés.
- Même chose pour le vecteur différence et le vecteur union.
- Eclater un vecteur V d'entiers positifs en 2 vecteurs A et B selon le critère ( premier ou pas). On utilisera le prédicat est-il-premier .
- Interclasser deux vecteurs ordonnés.
3. Algorithmes de mise à jour
- Insérer un élément donné après une valeur donnée du vecteur.
- Insérer un élément donné à la position p donnée du vecteur.
- Quelles modifications sont à faire dans les deux algorithmes précédents si le vecteur est ordonné.
- Supprimer logiquement un élément consiste à utiliser un champs additionnel pour la présence ou non de l’élément. Définir la structure du vecteur et écrire l'algorithme correspondant.
- Supprimer physiquement un élément consiste à l'éliminer complètement du vecteur. Ecrire l'algorithme correspondant.
4. Algorithmes de tri et mesure
Retrouver les algorithmes de tri correspondants aux méthodes présentées en cours :
- Tri par sélection
- Tri part selection et permutation
- Tri par Comptage
Mesurer chaque algorithme en dénombrant les comparaisons et les affectations portant uniquement sur les éléments du vecteur à trier.
5. Vecteur de vecteurs
- Triangle de Pascal
Construire le triangle de Pascal dans un tableau à deux dimensions. Ecrire la procédure Pascal qui l'imprime.
- Produit de 2 matrices.
Algorithme et programme Pascal correspondant.
- Histogramme
Une assemblée vote en choisissant une possibilité sur 6. Fabriquer dans un tableau à deux dimensions l'histogramme du vote. Ecrire la procédure Pascal qui l'imprime. Améliorer la solution en donnant des noms aux candidats.
- Résolution d'un système de n équations à n inconnues.
Algorithmes et programme Pascal.
- Calcul de la moyenne
Dans une classe de 30 élèves, en vue d'établir un classement à partir du tableau des notes obtenues en 9 compositions et des coefficients correspondants, calculer pour chaque élève la somme des produits de chaque note par son coefficient et la moyenne correspondante. Imprimer la liste des élèves par ordre de mérite. Algorithme et programme.