Partie 4.
Programmation modulaire
COURS 9 : Les actions composées
COURS 10 : Analyse descendante
COURS 11 : Communication entre modules
COURS 12 : Illustration de l'analyse descendante et la communication entre modules sur un exemple : Gestion de télégrammes.
Partie 4.
Programmation modulaire
COURS 9 :Les actions
composées ![]()
Considérons la formule Cnp = n ! / (p ! (n-p) ! )
L’algorithme qui calcule cette formule est le suivant :
| ALGORITHME CNP VAR R1, R2, R3, N, P, I : ENTIER BEGIN LIRE(N, P) R1 := 1 POUR I := 2, N R1 := R1 * I FINPOUR R1 := 2 POUR I := 2, P R2 := R2 * I FINPOUR R3 := 1 POUR I := 2, N-P R3 := R3 * I FINPOUR ECRIRE('Résultat : ', R1 / (R2*R3) ) FIN |
Nous remarquons dans cet algorithme que la séquence
R_ := 1
POUR I := 2, _
R_ := R_ * I
FINPOUR
Se répète 3 fois oł le symbole ‘_’ désigne les parties qui changent.
Afin d’éviter cette duplication, on crée une action composée puis il suffit de l’appeler plusieurs fois avec des données différentes que nous appellerons paramètres.
9.2 Actions composées
Quand une séquence d'actions se répète plusieurs fois dans un algorithme, il est avantageux et même nécessaire de créer une action composée (ou module). En langage algorithmique, on définit un module de la façon suivante :
| ACTION nom ( v1, v2, ) définition des paramètres d'entrée et de sortie définition des objets locaux DEBUT Corps FIN |
Au niveau de la définition de l’action, les paramètres sont dits formels.
La structure d'un algorithme devient alors :
| ALGORITHME nom Définition des objets Définition des modules DEBUT corps FIN |
L'appel se fait par N
Les paramètres sont appelés réels ou effectifs.
Nom ( p1, p2,....). |
Dans l'exemple précédent, on crée l'action Fact suivant :
| ACTION Fact (N, R) VAR I, N, R : ENTIER DEBUT R := N POUR I := N- 1, 2, -1 R := R * I FINPOUR FIN |
L'algorithme devient :
| ALGORITHME Cnp VAR N, P, R1, R2, R3, Result : ENTIER (* définition de l'action Fact *) ACTION Fact (N, R) VAR I, N, R : ENTIER DEBUT R := N POUR I := N- 1, 2, -1 R := R * I FINPOUR FIN DEBUT LIRE (N, P) Fact ( N, R1) Fact ( P,R2) Fact (N-P, R3) Result := ( R1 * R2 ) / R3 ECRIRE (Result ) FIN. |
Une fonction est définie comme suit :
| FONCTION Nom ( paramètres d'entrée ) : type Définition des paramètres et des objets locaux DEBUT corps FIN |
Une fonction est utilisée directement dans une expression.
Dans le corps de la fonction, il doit toujours exister une affectation du genre
‘Nom de la fonction := expression’
C’est cette valeur qui est retournée par la fonction.
La fonction associée au module Fact précédent est la suivante :
| FONCTION Fact ( N )
: ENTIER VAR N, I, R : ENTIER DEBUT R := N POUR I := N- 1, 2, -1 R := R * I FINPOUR Fact := R FIN |
l'algorithme devient :
| ALGORITHME CNP VAR N,P : ENTIER (* DEFINIR ICI LA FONCTION FACT *) DEBUT LIRE (N, P) ECRIRE ( (Fact (N)* Fact (N-P) ) / Fact (P) ) FIN |
Quand le résultat de l'action composé est unique et de type booléen, il est préférable d'écrire l'action composée sous la forme d'un prédicat.
| PREDICAT Nom ( paramètres ) Définition des paramètres et des objets locaux DEBUT Corps FIN |
Dans le corps d’un prédicat, il doit toujours exister une affectation du genre
‘Nom du prédicat := expression’
C’est cette valeur qui est retournée par le prédicat.
Exemple
| PREDICAT Egal ( A,
B) VAR A, B : ENTIER DEBUT Egal := (A=B) FIN |
l'algorithme qui suit utilise le prédicat Egal comme suit :
| ALGORITHME EXEMPLE VAR I, Cpt, A, N : ENTIER ; DEBUT Cpt := 0 POUR I := 1, N : LIRE( N) SI Egal (N, A) : Cpt := Cpt + 1 FSI FINPOUR FIN |
En pascal, on parle de PROCEDURE et FONCTION. Les prédicats sont des fonctions de type booléen. les paramètres sont définis dans les instructions procédures et fonctions. Un résultat d'une procédure doit être déclaré avec l’option VAR.
Définition d'une procédure
| PROCEDURE Nom ( [ VAR ] p1, p2, .... : type;
[ VAR ] p1, p2, .... : type; ..... ) En-tête BEGIN Corps END |
L'appel se fait
Nom (n1, n2,....) |
Exemple
| PROGRAM Cnp ; VAR N, P, R1, R2, R3, Result : INTEGER ; (* définition de l'action Fact *) PROCEDURE Fact (N, R) ; VAR I, N, R : INTEGER ; BEGIN R := N ; FOR I := N- 1 DOWNTO 2 R := R * I ; END ; BEGIN READ (N, P) Fact ( N, R1) Fact ( P,R2) Fact (N-P, R3) Result := ( R1 * R2 ) / R3 WRITE (Result ) END. |
Définition d'une fonction
| FUNCTION Nom ( p1, p2 ,.... : type, ect...) :
type VAR En-tête BEGIN Corps FIN |
Dans le corps, il doit exister au moins une affectation du genre Nom := valeur
Une fonction est utilisée directement dans une expression.
La définition est récursive : à son tour une procédure( ou fonction) peut contenir d'autres. Etc.
| ALGORITHME CNP VAR N,P : ENTIER (* définition de l'action Fact *) FUNCTION Fact (N : INTEGER) : INTEGER; VAR I, N, R : INTEGER ; BEGIN R := N ; FOR I := N- 1 DOWNTO 2 R := R * I ; Fact := R END ; BEGIN READ (N, P) WRITE ( (Fact (N)* Fact (N-P) ) / Fact (P) ) END. |
COURS 10 : Analyse
descendante ![]()
Objectifs : diviser un problème en sous problèmes pour régner, telle est la devise de l’analyse descendante, construire des modules ou des actions composées quand la technique de l’analyse descendante est employée pour la résolution d’un problème.
10.1 Définition
L’analyse descendante est un mode de pensée visant à construire des algorithmes en partant d'un niveau très général et en détaillant peu à peu chaque traitement, jusqu'à arriver au niveau de description le plus bas.
10.2 Caractéristique
C’est une méthode permettant d'aborder un problème, de reconnaître sa structure et donc les traitements qu'il faudra mettre en œuvre pour le résoudre.
10.3 Technique
On peut énoncer la technique de l’analyse descendante comme suit :
(i) - Utilisation des structures de contrôle
(ii) - Essai de reconnaître dans un problème les traitements permettant de se ramener à un problème connu. Laisser à part les problèmes complexes P1, P2, ...
(iii) - Application itérative de (i) et (ii) jusqu'à arriver au niveau le plus bas.
A chaque étape, on suppose qu'il existe une machine abstraite capable de traiter les Pi.
La construction d'un algorithme par la méthode d'analyse descendante revient à définir des machines abstraites dont le fonctionnement est décrit par des algorithmes adaptés à chaque niveau de machine.
10.4 Exemple
Le problème : décomposer une liste de N nombres en facteur premier.
Première étape
On ne s’occupe que du problème du parcours des données.
| POUR I :=1, N : LIRE(Nombre) Décomposer le nombre Nombre en facteur premier FINPOUR |
Deuxième étape
Il s’agit de la décomposition d’un nombre. Pour cela, on parcours tous les nombres premiers de 2 à Nombre/2 en vue de déterminer les exposants.
| Premiercourant := 2 TANTQUE Premiercourant <= Nombre Déterminer l'exposant Exposant Si Exposant <> 0 ECRIRE(Premiercourant, Exposant) FSI Déterminer le prochain nombre premier, soit Premiercourant FINTANTQUE |
Troisième étape
Il s’agit de rechercher l’exposant associé à un nombre premier. Comme on est au niveau le plus bas, on donne l’algorithme au détail.
| ACTION Exposant (
Nombre, Premiercourant, Exposant) VAR Divise : BOOLEEN Exposant, Premiercourant DEBUT Divise := Vrai Exposant := 0 ; TANTQUE Divise A := Nombre / Premiercourant SI A * Premiercourant = Nombre Exposant := Exposant + 1 Nombre := A FSI FINTANTQUE FIN |
Quatrième étape
Nous devons rechercher le prochain nombre premier à partir d’un nombre premier, soit Premiercourant.
| I := Premiercourant + 2 TANTQUE I n'est pas un nombre premier I := I + 2 FINTANTQUE |
Remarquer que nous prenons que les nombres impaires comme candidats pour le test : premier ou pas.
Cinquième étape
Il s’agit de reconnaître un nombre premier. Comme on est au niveau le plus bas de l’analyse on done l’algorithme en détail. De plus, comme le résultat est booléen, nous l’écrivons sous forme de prédicat.
| PREDICAT
Estilpremier (Nombre) VAR Divisible : BOOLEEN J, A, Quotient, Nombre : ENTIER DEBUT J := 2 Divisible := FAUX A := Nombre / 2 TANTQUE j <= A et NON Divisible Quotient := Nombre DIV J SI Quotient * J = Nombre Divisible := VRAI SINON J := J + 1 FSI FINTANTQUE Estimpremier := NON Divisible FIN |
Cours 11.
Communication entre modules ![]()
Objectifs : introduire la notion de portée des objets, donner deux moyens de communication entre modules : par paramètres et variables globales.
11.1 Nomenclature
Dans notre contexte le mot bloc désigne soit un algorithme soit un module ( action, fonction ou prédicat)
Soit la structure de l'algorithme suivante:
M1 [ a, b,
c, d
M2 [c, d, e
M3 [ a, b
]
M4 [ d, e
]
]
]
On définit les termes suivants :
blocs parallèles, blocs disjoints : M1 et M3 sont des blocs disjoints
bloc contenant un autre bloc : M1 contient M2
bloc contenu dans un autre bloc : M4 est contenu dans M2
bloc intérieur à un autre bloc : M3 est un bloc intérieur à M1
bloc extérieur à un autre bloc : M1 est un bloc extérieur à M2.
blocs emboîtés, bloc imbriqués : M1, M2 et M3 sont dits emboîtés.
Tout objet défini dans un bloc est dit local à ce bloc. Il n'est pas connu à l'extérieur de ce bloc.
Tout objet défini dans un bloc est connu dans tous bloc intérieur à ce bloc sauf s'il est redéfini. On dira qu'il est global à ces blocs intérieurs.
11. 2 Portée des objets
On désigne par portée d’un objet le domaine de visibilité de l’objet. C’est donc l’ensemble des blocs ou l’objet est connu. Dans l’exemple précédent, les portées des objets sont données dans la table suivante :
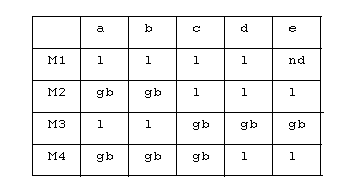
l désigne local, gb globale et nd non défini.
11.3 Communication entre modules
La communication entre les modules peut se faire :
- a l'aide de paramètre
- à l'aide de variables globales
Nous reviendrons sur des exemples plus loin.
COURS 12 :
Illustration de l'analyse descendante et la communication entre modules sur un exemple :
Gestion de télégrammes. ![]()
Objectifs : illustrer les notions de module, d’analyse descendante et de communication entre modules à travers un exemple.
12.1 Enoncé
Sur le ruban de la machine caractère se trouve une suite de télégrammes. Chaque télégramme est terminé par le mot 'FINTEL'. Chaque télégramme est constitué de mots( suite de caractères non blanc) séparés par un ou plusieurs blancs. Ces mots sont divisés en catégories :
- les mots à facturer
- les mots de service non facturables qui sont 'STOP' et 'FINTEL'.
La suite de télégrammes est terminée par le télégramme vide ( télégramme ne contenant aucun mot ou que des 'STOP')
Ecrire un algorithme, qui pour chaque télégramme, imprime le texte du télégramme ( les mots étant séparés par un seul blanc) suivi du nombre de mots à facturer et du nombre de mots dépassant 12 caractères. Ces mots seront tronqués dans le texte imprimé.
Exemple de télégramme : « Bonjour stop je souhaite bon courage à tout le monde stop stop fintel stop fintel »
12.2 Les différents modules
Le premier problème qui nous préoccupe est celui de parcours des télégrammes. Supposons qu’on dispose du module Traiter_télégramme qui permet de reconnaître un télégramme et de nous revoyer deux valeurs F et K désignant respectivement le nombre de mots facturables et le nombre de mots de longueur supérieure à 12.
On peut alors exprimer l’algorithme comme suit :
Algorithme_principal
| Telegrammenonvide := VRAI TANTQUE Telegrammenonvide : Traiter_telegramme ECRIRE(F, K) Telegrammenonvide := NON (f=0) FINTANTQUE |
De même, on essaye de résoudre le problème de parcours au sein même d’un télégramme. Pour cela considérons les deux modules suivants : l’un permet d’obtenir le mot suivant et l’autre permet de le traiter.
L’algorithme correspondant à Traiter_telegramme est donc
Traiter_telegramme
| F := 0 K := 0 Nonfindetelegramme := VRAI TANTQUE Nonfindetelegramme : Obtenir_mot Traiter_mot FINTANTQUE |
Il nous reste plus qu’à détailler les deux modules :
Obtenir_mot
Il permet de récupérer le prochain mot et détermine sa longueur.
| LIRE(C) I := 0 Mot := '' TANTQUE C= ' ' : LIRE(C) FINTANTQUE TANTQUE C <> ' ' : I := I + 1 SI I <= 12 : Mot := Mot + C FSI LIRE(C) FINTANTQUE |
Traiter_mot
Ce module compte le nombre de mots facturables et ceux dont la longueur est supérieure à 12.
| ECRIRE ( Mot) SI Mot <> 'Fintel' et Mot <> 'Stop' : F := F + 1 FSI SI I > 12 : K := K + 1 FSI SI Mot = 'Fintel' : Nonfindetelegramme := FAUX FSI |
12.3 Rédaction de la solution
On peut rédiger la solution de diverses façons. Pour chaque cas donnons la structure modulaire et le programme PASCAL correspondant.
12.3.1 Communication par variables globales
[Algorithme F, K, TELEGRAMMEVIDE
[Traiter-telegramme I, MOT, NONFINDETELEGRAMME
[Obtenr-mot C
]
]
[Traiter-mot
]
]
F, K et Telegrammenonvide sont des variables globales aux modules Traiter_telegramme, Obtenir_mot et Traiter_mot
I, Mot et Nonfindetelgramme sont des variables locales du module Traiter_telegramme et globales aux modules Obtenir_mot et Traiter_mot.
C est une variable locale au module Obtenir_mot.
Programme PASCAL correspondant :
| PROGRAM Telegrammes; TYPE Tchaine = STRING[12]; VAR F, K : INTEGER; Telegrammenonvide : BOOLEAN; Fe, Fs : TEXT; PROCEDURE Traiter_telegramme; VAR I : INTEGER; Mot : Tchaine ; Nonfindetelegramme : BOOLEAN; PROCEDURE Obtenir_mot; VAR C : CHAR; BEGIN READ(Fe, C); Mot := ''; I := 0; WHILE C =' ' DO READ(Fe, C); WHILE (C <> ' ') DO BEGIN I := I + 1; IF I <= 12 THEN Mot := Mot + C ; READ(Fe, C) END; END; PROCEDURE Traiter_mot ; BEGIN WRITE(Fs, Mot, ' '); IF (Mot <> 'FINTEL') AND (Mot <> 'STOP') THEN F := F + 1; IF I > 12 THEN K:= K + 1 ; IF Mot = 'FINTEL' THEN Nonfindetelegramme := FALSE END; BEGIN F := 0; K := 0; Nonfindetelegramme := TRUE; WHILE Nonfindetelegramme DO BEGIN Obtenir_mot; Traiter_mot END; END; BEGIN ASSIGN(Fe, 'D_telegr.Pas'); ASSIGN(Fs, 'R_telegr.Pas'); RESET(Fe); REWRITE(Fs); Telegrammenonvide := TRUE; WHILE Telegrammenonvide DO BEGIN Traiter_telegramme; WRITELN(Fs, 'F=', F, ' K=',K) ; Telegrammenonvide := NOT ( F=0) END; CLOSE(Fs); END. |
12.3.2 Communication par paramètres
[Algorithme
Freel, Kreel, Telegrammenonvidereel
[Traiter-telegramme (Fformel, Kformel)
Ireel, Motreel,
Nonfindetelegrammereel
[Obtenr-mot ( Iformel,
Motformel)
C
]
]
[Traiter-mot(Iformel,Motformel, Fformel, Kformel,
Nonfindetelegrammeformel
]
]
Freel, Kreel, Telegrammenonvidereel sont des variables locales de l’algorithme
principal.
Ireel, Motreel, Nonfindetelegrammereel sont des variables locales du module traiter_telegramme.
C est une variable locale du module Obtenir_Mot.
Programme PASCAL correspondant :
| PROGRAM Telegrammes; TYPE Tchaine = STRING[12]; VAR Freel, Kreel : INTEGER; Telegrammenonvidereel : BOOLEAN; Fe, Fs : TEXT; PROCEDURE Traiter_telegramme ( VAR Fformel, Kformel : INTEGER) ; VAR Ireel : INTEGER; Motreel : Tchaine; Nonfindetelegrammereel : BOOLEAN; PROCEDURE Obtenir_mot ( VAR Iformel : INTEGER; VAR Motformel :Tchaine ); VAR C : CHAR; BEGIN READ(Fe, C); Motformel := ''; Iformel := 0; WHILE C =' ' DO READ(Fe, C); WHILE (C <> ' ') DO BEGIN Iformel := Iformel + 1; IF Iformel <= 12 THEN Motformel := Motformel + C ; READ(Fe, C) END; END; PROCEDURE Traiter_mot (Iformel : INTEGER; Motformel : Tchaine; VAR Fformel, Kformel : INTEGER; VAR Nonfindetelegrammeformel : BOOLEAN); BEGIN WRITE(Fs, Motformel, ' '); IF (Motformel <> 'FINTEL') AND (Motformel <> 'STOP') THEN Fformel := Fformel + 1; IF Iformel > 12 THEN Kformel:= Kformel + 1 ; IF Motformel = 'FINTEL' THEN Nonfindetelegrammeformel := FALSE END; BEGIN Freel := 0; Kreel := 0; Nonfindetelegrammereel := TRUE; WHILE Nonfindetelegrammereel DO BEGIN Obtenir_mot (Ireel, Motreel); Traiter_mot(Ireel, Motreel, Freel, Kreel, Nonfindetelegrammereel ) END; END; BEGIN ASSIGN(Fe, 'D_telegr.Pas'); ASSIGN(Fs, 'R_telegr.Pas'); RESET(Fe); REWRITE(Fs); Telegrammenonvidereel := TRUE; WHILE Telegrammenonvidereel DO BEGIN Traiter_telegramme (Freel, Kreel); WRITELN(Fs, 'F=', Freel, ' K=',Kreel) ; Telegrammenonvidereel := NOT ( Freel=0) END; CLOSE(Fs); END. |
12.3.3 Communication par paramètres et par variables globales
[Algorithme
Fglobal, Kglobal, Telegrammenonvideglobal
[Traiter-telegramme
Ireel, Motreel,
Nonfindetelegrammereel
[Obtenr-mot ( Iformel,
Motformel)
C
]
]
[Traiter-mot(Iformel,
Motformel, Nonfindetelegrammeformel )
]
]
Fglobal, Kglobal, Telegrammenonvideglobal sont des variables locales de l’algorithme principal et sont donc globales à tous les modules.
Ireel, Motreel, Nonfindetelegrammereel sont des variables locales du module Traiter_telegramme.
C est une variable locale du module Obtenir_Mot.
Programme PASCAL correspondant :
| PROGRAM Telegrammes; TYPE Tchaine = STRING[12]; VAR Fglobal, Kglobal : INTEGER; Telegrammenonvidereel : BOOLEAN; Fe, Fs : TEXT; PROCEDURE Traiter_telegramme ; VAR Ireel : INTEGER; Motreel : Tchaine; Nonfindetelegrammereel : BOOLEAN; PROCEDURE Obtenir_mot ( VAR Iformel : INTEGER; VAR Motformel : Tchaine ); VAR C : CHAR; BEGIN READ(Fe, C); Motformel := ''; Iformel := 0; WHILE C =' ' DO READ(Fe, C); WHILE (C <> ' ') DO BEGIN Iformel := Iformel + 1; IF Iformel <= 12 THEN Motformel := Motformel + C ; READ(Fe, C) END; END; PROCEDURE Traiter_mot (Iformel : INTEGER; Motformel : Tchaine; VAR Nonfindetelegrammeformel : BOOLEAN); BEGIN WRITE(Fs, Motformel, ' '); IF (Motformel <> 'FINTEL') AND (Motformel <> 'STOP') THEN Fglobal := Fglobal + 1; IF Iformel > 12 THEN Kglobal:= Kglobal + 1 ; IF Motformel = 'FINTEL' THEN Nonfindetelegrammeformel := FALSE END; BEGIN Fglobal := 0; Kglobal := 0; Nonfindetelegrammereel := TRUE; WHILE Nonfindetelegrammereel DO BEGIN Obtenir_mot (Ireel, Motreel); Traiter_mot(Ireel, Motreel, Nonfindetelegrammereel ) END; END; BEGIN ASSIGN(Fe, 'D_telegr.Pas'); ASSIGN(Fs, 'R_telegr.Pas'); RESET(Fe); REWRITE(Fs); Telegrammenonvidereel := TRUE; WHILE Telegrammenonvidereel DO BEGIN Traiter_telegramme ; WRITELN(Fs, 'F=', fglobal, ' K=',Kglobal) ; Telegrammenonvidereel := NOT ( Fglobal=0) END; CLOSE(Fs); END. |
Remarque
Les trois programmes présentés admettent comme fichier de données (D_telegr.pas) contenant le texte suivant :
Bonjour STOP commencer à programmer en PASCAL STOP bon courage à tout le monde FINTEL réfléchissez avant de commencer STOP FINTEL STOP STOP N'oubliez pas de remettre un rapport FINTEL STOP FINTEL FINTEL
Et comme résultats (R_telegr.pas)
Bonjour STOP commencer à programmer en PASCAL STOP bon courage à tout le monde FINTEL F=12 K=0
réfléchissez avant de commencer STOP FINTEL F=4 K=0
STOP STOP N'oubliez pas de remettre un rapport FINTEL F=6 K=0
STOP FINTEL F=0 K=0
1. Ecrire les prédicats suivants :
(a) Egal(a, b) : vrai si a=b
(b) Parfait(a) : vrai si a un nombre parfait. ( Un nombre a est parfait s'il est égal à la somme de ses diviseurs, a exclu )
Utiliser ces prédicats pour déterminer dans une liste de nombres( machine-nombres) d'abord le nombre de doubles d'un nombre a donné puis les nombres parfaits.
2. Ecrire la fonction factorielle, puis l'utiliser pour écrire l'algorithme qui imprime le triangle de Pascal.
3. Calculer l'expression ( Sin x + Sin 3x ) / Sin 4x avec Sin x = x - x3/3! + x5/5! - ..... (-1)k x 2k+ 1 / (2k+1)! en prenant n termes, n donné.
4. Considérons une liste de N nombres entiers ( N > 1). On veut écrire un seul algorithme qui répond aux questions suivantes :
- déterminer le troisème nombre premier s'il existe,
- déterminer le deuxième carré parfait s'il existe,
- déterminer le nombre de diviseurs du premier nombre pair et du dernier nombre impair.
Utiliser les modules suivants pour écrire cet algorithme :
- prem( nombre ) : prédicat égal à vrai si nombre est premier, faux sinon.
- carré (nombre) : prédicat égal à vrai si nombre est carré parfait, faux sinon.
- nbdiv(nombre) : fonction qui donne le nombre de diviseurs de nombre.
- pair(nombre) : prédicat égal à vrai si nombre est pair, faux sinon.
Ecrire le programme Pascal correspondant
5. Reprendre le problème traité en cours sur la décomposition d'une suite de K nombres en facteurs premiers.
a) Donner une solution uniquement avec les variables globales. Toutes les actions composées sont alors SANS paramètres.
b) Donner une solution mixte possible ( avec paramètres et variables globales ( ou communes )
c) Rédiger la solution en procédant par différentes manières. Programmer les différentes versions en PASCAL.
6. Donner la portée de toutes les variables définies dans la structure algorithmique suivante :
ALGORITHME Portee
VAR
A, B, C, D, E : ENTIER
X, Y, Z, T : BOOLEEN
ACTION A1
VAR
A, B : CAR
T : REEL
DEBUT
.....
FIN
ACTION A2 ( T )
VAR
T, E : ENTIER
ACTION A3 ( A, B )
VAR
A, B : ENTIER
Z,Y : REEL
DEBUT
....
FIN
DEBUT
.....
FIN
DEBUT
...
FIN