Sommaire Définition du langage d’expérimentation Compilateur pour le langage Z minimal Extensions du langage Z minimal
Chapitre précédent Chapitre 17 : Machines de Turing Chapitre suivant
17.5 Exemple 1 (Machine_caractères)
17.6 Exemple 2 (Machine-nombres)
17.1 Introduction
![]()
On définit deux machines rudimentaires de Turing : machine-caractères et machine-nombres. Ces machines dotées d’opérations élémentaires permettant l’écriture des algorithmes simples afin de s’initier à l’algorithmique. Ces machines offrent les opérations CREER_MCAR, LIRECAR et NBRCAR sur la machine-caractères et les opérations CREER_MNOMBRE, LIRENOMBRE et NBRNOMBRE sur la machine-nombres.
La sémantique consiste à définir d’une part les quadruplets nécessaires correspondant aux opérations des deux machines et d’autre part déterminer l’emplacement des fonctions sémantiques dans les règles de grammaire ainsi que leur description en détail.
Rappelons que l’utilisation des quadruplets facilite leur interprétation ou leur génération de code.
17.2 Quadruplets
![]()
Pour la machine-caractères avec les opérations CREER_MCAR(M, [Chaine]), LIRECAR(M,Caractere) et NBRCAR(M), les quadruplets suivants sont à générer:
- (‘Créer_mcar’, A, B, )
A : pointeur TABOB vers l’objet machine-caractères.
B : pointeur dans TABOB vers la constante chaîne de caractères.
L’objet machine-caractères aura ‘Mc’ comme code pour son type.
- (‘Lirecar’, A, B, )
A : pointeur dans TABOB vers l’objet machine-caractères.
B : pointeur dans TABOB vers l’objet qui recevra la donnée lue.
- (‘Nbrcar’, A, ,C )
A : pointeur dans TABOB vers l’objet machine-caractères.
C : pointeur dans TABOB vers le résultat.
Pour la machine-nombres avec les opérations CREER_ MNOMBRE (M , [ Exp1 , Ex p2 , … ]) , LIRENOMBRE(M, Nombre) et NBRNOMBRE(M) les quadruplets suivants sont à générer:
- (‘Créer_mnombre’, A, B, C )
A : pointeur dans TABOB vers l’objet machine-nombres.
B : pointeur dans TABCOMP vers la liste des expressions.
C : nombre d’expressions.
L’objet machine-nombres aura ‘Mn’ comme code pour son type.
- (‘Lirenombre’, A, B, )
A : pointeur dans TABOB vers l’objet machine-nombres.
B : pointeur dans TABOB vers l’objet qui recevra la donnée lue.
- (‘Nbrnombre’, A, ,C )
A : pointeur dans TABOB vers l’objet machine-nombres.
C : pointeur dans TABOB vers le résultat.
17.3 Syntaxe
![]()
Notre grammaire est étendue comme suit avec les règles en surbrillance portant sur les machines considérées:
Déclarations
<Algo Z> → [ ~Soit|Soient~ <Ps> ] Debut <Lis> Fin [;] { ~<Act> | <Fonct>~ [;] }*
<Act> → Action Idf [ ( <Li> ) ] [;] [ ~Soit|Soient~ <Ps> ] Debut <Lis> Fin
<Fonct> → Fonction Idf ( <Li> ) : <Typ> [ ~Soit|Soient~ <Ps> ] Debut <Lis> Fin
<Ps> → <S>;{ [~Soit|Soient~] <S>;}*
<S> → <Li> Sep ~<Typ>|~Action|Fonction(<Typ>)~ ~
<Li> → Idf {, Idf}*
<Typ> → Types | <Structsimple> | <Structcomplexe> |
Machine_car | Machine_nombre |
Tableau (<Lc>) [De~<Structsimple> | Types~ ] |
<Structsimple> → [Structure ](Types {, Types }*)
<Structcomplexe>→ [Structure ]( ~ Types| Vecteur(Cste) [De Types] ~ {, ~ Types | Vecteur(Cste) [De Types] ~ }*)
<Lc> → Cste {, Cste}*
Instructions
< Lis > → < Inst > { ; < Inst > }*
<Inst> → Idf := <Exp> |
Lire ( Idf {, Idf }* ) |
Ecrire (<Exp> {,<Exp>}* ) |
Tantque <Exp> [ : ] <Lis> Fintantque |
Si <Exp> [:] <Lis> [Sinon <Lis>] Fsi |
Pour Idf:= <Exp>,<Exp> [, <Exp>][:] <Lis> Finpour |
Appel Idf [(Exp {,<Exp>}*)]
~ Creer_liste | Init_vecteur | Init_struct |
Creer_mnombre ~
( Idf , [[ ~<Exp>|[[<Exp> {, <Exp>}*]] ~
{, ~<Exp>|[[<Exp> {, <Exp>}*]]~}* ]] ) |
Aff_element ( <Exp> [[ <Exp> {, <Exp> }* ]] ,<Exp> ) |
Creer_mcar(Idf, [[ Chaine ]]) |
~Lirecar|Lirenombre~ (Idf, Idf) |
Aff_struct(Idf, Cste, <Exp>)
Expressions
<Exp> → <Exps>[ Opr <Exps>]
<Exps> → [Sign] <Terme> { Opa <Terme> }*
<Terme> → <Facteur>{Opm <Facteur>}*
<Facteur> → Idf [(Exp {,<Exp>}*)] | Cste | ( <Exp>) | <Fonct> | Non <Facteur> | Vrai | Faux | Chaine
<Fonct> → Element ( <Fonct> [[ <Exp> {, <Exp> }* ]] ) | Struct ( Idf, Cste) |
~Nbrcar|NbrNombre~ (Idf)
17.4 Fonctions sémantiques
![]()
Déclaration
<Typ> → Machine_car F1 | Machine_nombre F2
F1
Récupérer le type de la machine-caractères. Type = ‘MC’
F2
Récupérer le type de la machine-nombres. Type = ’MN’
Creer-mnombre
<Inst> → Creer_mnombre ( Idf F1 , [[ <Exp> F2 {, <Exp> F3 }* ]] ) F4
F1
Si le type de Idf est différent de 'MN' alors Erreur. Soit Ptidf l’objet créé dans TABOB pour Idf.
F2
Soit Temp le résultat de <Exp>.
Si Temp n’est pas un entier : Erreur.
Nb=1; Mettre Temp dans TABCOMP (table complémentaire). Soit Deb sa position dans cette table.
F3
Soit Temp le résultat de <Exp>.
Si Temp n’est pas un entier Erreur.
Nb=Nb+1; Mettre Temp dans TABCOMP.
F4
Générer le quadruplet ( ‘Creer_mnombre’, Ptidf, Deb, Nb).
Creer_mcar
<Inst> → Creer_mcar(Idf F1 , [[ Chaine F2 ]]) F3
F1
Si le type de Idf est différent de 'MC' alors Erreur. Soit Ptidf l’objet créé dans TABOB pour Idf.
F2
Mettre Chaine dans la table des constantes TABCONS. Soit Ptcons son indice dans cette table.
F3
Générer le quadruplet ( ‘Creer_mcar’, Ptidf, Ptcons, )
Lirecar et Lirenombre
<Inst> → ~Lirecar F1 | Lirenombre F1 ~ (Idf F2 , Idf F3 ) F4
F1
Sauv = Sem. C’est l’unité lexicale venant d’être reconnue.
F2
Si Sauv= ‘Lirecar’ et le type de Idf est différent de ‘MC’ : Erreur.
Si Sauv= ‘Lirenombre’ et type de Idf est différent de ‘MN’ : Erreur.
Soit Ptidf1 l’indice de Idf dans TABOB.
F3
Si Sauv= ‘Lirecar’ et type de Idf est différent de ‘C’ : Erreur.
Si Sauv= ‘Lirenombre’ et type de Idf est différent de ‘E’ : Erreur.
Soit Ptidf2 l’indice de Idf dans TABOB.
F4
Générer le quadruplet (Sauv, Ptidf1, Ptidf2, )
Nbrcar et Nbrnombre
<Fonct> → ~Nbrcar F1 | NbrNombre F1 ~ (Idf F2 ) F3
F1
Sauv = Sem.
F2
Si Sauv= ‘Nbrcar’ et type de Idf est différent de ‘MC’ : Erreur.
Si Sauv= ‘Nbrnombre’ et type de Idf est différent de ‘MN’ : Erreur.
Soit Ptidf l’indice de Idf dans TABOB.
F3
Générer un temporaire Temp où sera rangé le résultat. Générer le quadruplet (Sauv, Ptidf, , Temp)
17.5 Exemple 1 (Machine_caractères)
![]()
La figure 34 montre les tables de compilation générées pour le programme source donné.
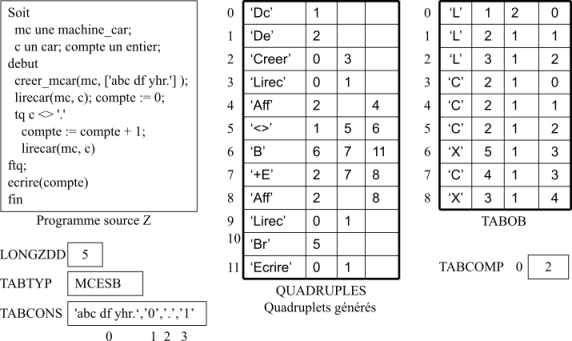
Figure 34: Tables de compilation(Machine_caractères)
17.6 Exemple 2 (Machine-nombres)
![]()
La figure 35 montre les tables de compilation générées pour le programme source donné.
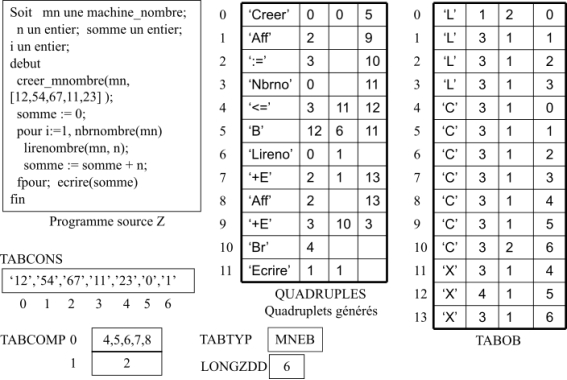
Figure 34: Tables de compilation (Machine_nombres)
17.7 Interprétation
![]()
L’interprétation consiste à choisir une représentation pour chaque type de machine et de traduire les quadruplets correspondants.
Nous pouvons opter pour les deux implémentations suivantes (exprimées en PASCAL)
Implémentation de la Machine-Caractères
TYPE Typemcar = ^Elementmcar;
Elementmcar = RECORD
Chaine : STRING(255) ;
Nombre : INTEGER;
Indice_courant : INTEGER
END;
La machine est une chaîne de caractères. Nous maintenons deux champs. L’un (Nombre) indique le nombre de caractères dans la chaîne et l’autre (Indice_courant) indique l’indice du caractère courant. Chaque opération de lecture incrémente cet indice pour récupérer le caractère de rang Indice_courant dans la chaîne.
Implémentation de la Machine-nombres
TYPE Typemnombre = ^Elementmnombre;
Elementmnombre = RECORD
Adrvect : POINTER ; // vers un tableau alloué dynamiquement
Nombre : INTEGER;
Indice_courant : INTEGER
END;
La machine est un tableau dynamique d’entiers. Nous maintenons deux champs. L’un (Nombre) indique le nombre de nombres dans le tableau et l’autre (Indice_courant) indique l’indice du nombre courant. Chaque opération de lecture incrémente cet indice pour récupérer le nombre de rang Indice_courant dans le tableau.