Sommaire Définition du langage d’expérimentation Compilateur pour le langage Z minimal Extensions du langage Z minimal
Chapitre précédent Chapitre 16 : Structures complexes Chapitre suivant
16.2 Représentation d’une structure complexe en mémoire
16.4 Table des objets : (TABOB )
16.1 Introduction
![]()
On distingue deux types de structure (enregistrement ) :
- Structure simple : ensemble de champs de type simple (ENTIER, BOOLEEN, CAR, CHAINE).
- Structure complexe : ensemble de champs de type simple ou de champ de type TABLEAU à une dimension de type simple.
La sémantique des structures simples et des tableaux revient à donner une solution aux problèmes suivants:
- Comment représenter une structure complexe en mémoire?
- Comment coder les structures complexes?
- Comment les mettre dans la table des objets?
- quels sont les quadruplets à générer?
- Où insérer les fonctions sémantiques dans les règles?
- Quelle est la description des fonctions sémantiques?
- Comment seront interpréter les quadruplets générés?
Dans ce qui suit nous donnons des solutions à tous les problèmes posés.
16.2 Représentation d’une structure complexe en mémoire
![]()
La figure 32 montre comment une structure complexe est représentée en mémoire. A toute structure complexe est associé un descriptif qui contient autant de mots que de champs dans la structure complexe. Dans la figure, le descriptif adresse un autre descriptif qui est celui d’un tableau.
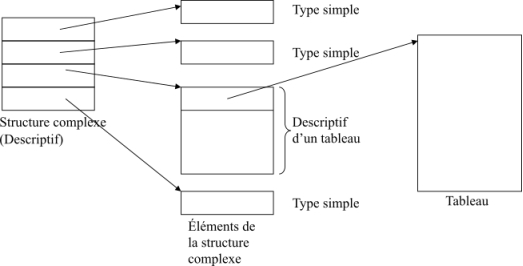
Figure 32: Représentation mémoire d’une structure complexe
16.3 Table des types (TABTYP)
![]()
Une structure complexe est codée comme une structure simple, c’est dire de la manière suivante:
‘(’ , suivi des types de ses champs et de ‘)’.
Exemples
Une structure complexe ayant pour champs un entier, une chaîne de caractères, un tableau(10, 10) de booléens et un entier est codée en (EST10,10BE).
La sémantique d’une déclaration de structure complexe consiste à former son type et le ranger dans la table des types s’il n’existe pas.
16.4 Table des objets : (TABOB )
![]()
La table des objets est utilisée telle quelle. Le champ Type désigne le rang de la sous chaîne de caractères formant le type dans la table des types TABTYP et le champ Nombre désigne la longueur du type (nombre de caractères formant le type).
16.5 Quadruplets
![]()
Les quadruplets sont les mêmes que ceux définis sur les structures simples.
16.6 Syntaxe
![]()
La grammaire courante étendue avec les structures complexes (en surbrillance) est la suivante :
Déclarations
<Algo Z> → [ ~Soit|Soient~ <Ps> ] Debut <Lis> Fin [;] { ~<Act> | <Fonct>~ [;] }*
<Act> → Action Idf [ ( <Li> ) ] [;] [ ~Soit|Soient~ <Ps> ] Debut <Lis> Fin
<Fonct> → Fonction Idf ( <Li> ) : <Typ> [ ~Soit|Soient~ <Ps> ] Debut <Lis> Fin
<Ps> → <S>;{ [~Soit|Soient~] <S>;}*
<S> → <Li> Sep ~<Typ>|~Action|Fonction(<Typ>)~ ~
<Li> → Idf {, Idf}*
<Typ> → Types | <Structsimple> | <Structcomplexe> | Tableau(<Lc>)[De~<Structsimple>|Types~ ]
<Structsimple> → [Structure ](Types {, Types }*)
<Structcomplexe> → [Structure ] ( ~ Types | Vecteur(Cste) [De Types] ~ {, ~ Types | Vecteur(Cste) [De Types] ~ }*)
<Lc> → Cste {, Cste}*
Instructions
< Lis > → < Inst > { ; < Inst > }*
<Inst> → Idf := <Exp> |
Lire ( Idf {, Idf }* ) |
Ecrire (<Exp> {,<Exp>}* ) |
Tantque <Exp> [ : ] <Lis> Fintantque |
Si <Exp> [:] <Lis> [Sinon <Lis>] Fsi |
Pour Idf:= <Exp>,<Exp> [, <Exp>][:] <Lis> Finpour |
Appel Idf [(Exp {,<Exp>}*)]
~ Init_vecteur | Init_struct ~ ( Idf , [[ ~<Exp>|[[<Exp> {, <Exp>}*]] ~ {, ~<Exp>|[[<Exp> {, <Exp>}*]]~}* ]] ) |
Aff_element ( <Exp> [[ <Exp> {, <Exp> }* ]] ,<Exp> ) |
Aff_struct(Idf, Cste, <Exp>)
Expressions
<Exp> → <Exps>[ Opr <Exps>]
<Exps> → [Sign] <Terme> { Opa <Terme> }*
<Terme> → <Facteur>{Opm <Facteur>}*
<Facteur> → Idf [(Exp {,<Exp>}*)] | Cste | ( <Exp>) | <Fonct> | Non <Facteur> | Vrai | Faux | Chaine
<Fonct> → Element ( <Fonct> [[ <Exp> {, <Exp> }* ]] ) | Struct ( Idf, Cste)
16.7 Fonctions sémantiques
![]()
Déclaration
Le rôle des fonctions sémantiques est de construire la chaîne de caractères formant le type.
<Structcomplexe> → [Structure ] ( ~ Types F1 |
Vecteur F2 (Cste F3 ) [De Types F4 ] F5 ~ {, ~ Types F4 |
Vecteur F2 (Cste F3 )[De Types F4 ] F5 ~ }* ) F6
F1
Si Sem =’Chaine’ Faire Type=‘(S‘ sinon Type=‘(‘+Sem[1].
F2
Faire Type= Type + ‘V’.
F3
Vérifier que la constante Cste est positive. Faire Type=Type +Sem.
F4
Si Sem =’Chaine’ Faire Type=Type +‘S‘ sinon Type=Type + Sem[1].
F5
Si le dernier de Type est un chiffre faire Type = Type +’E’.
F6
Faire Type= Type + ‘)’.
Spécification de structure complexe
<S> → <Li> [ Sep <Typ> ] F1
F1
Soit L la liste produite par <Li> et soit Type le type produit par <Typ>.
Ranger Type dans TABTYP si Type n’existe pas. Soit I son indice dans cette table.
Pour chaque Idf dans L :
- Le mettre dans la table des symboles;
- Lui attribuer une adresse relative A et le mettre dans la table des objets (soit Pt son emplacement). L’objet créé aura comme Statut=‘L’;Type=I; Nombre=Longueur de Type et Adresse=A; Générer le quadruplet (‘Ds’, Pt, , )
16.8 Exemple
![]()
La figure 33 montre les tables de compilation produites par la phase sémantique. Le quadruplet de nom ‘Ds’ adresse dans son second paramètre l’objet 0 dans TABOB qui est un local désignant une structure complexe dont le type est rangé dans TABTYP à la position 1 et est de longueur 7.
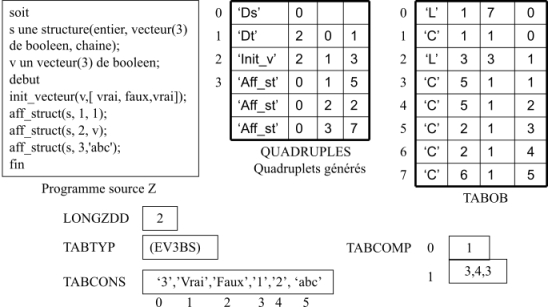
Figure 33: Tables de compilation(Structures complexes)
16.9 Interprétation
![]()
A la rencontre du quadruplet (‘Ds’, A, B, C) dans lequel A désigne l’objet structure complexe les opérations suivantes sont effectués:
- Allocation de l’espace mémoire pour chaque champ de la structure complexe.
- L’adresse de cet espace est rangé dans le descriptif de la structure complexe.
Si l’un des champs est un tableau, il faudrait allouer un espace pour les éléments du tableau et un espace pour mettre le descriptif du tableau. C’est l’adresse de ce descriptif de tableau qu’il faut mettre dans le descriptif de la structure complexe dans le champ approprié.
L’interprétation des quadruplets définis sur les structures simples s’applique sur les structures complexes.