Sommaire Définition du langage d’expérimentation Compilateur pour le langage Z minimal Extensions du langage Z minimal
Chapitre précédent Chapitre 18 : Listes linéaires chaînées Chapitre suivant
18.1 Introduction
![]()
On définit une machine abstraite sur les listes linéaires chaînées permettant l’initiation aux structures dynamiques de données. Cette machine abstraite offre les opérations de base sur les listes : ALLOUER , LIBERER , VALEUR, SUIVANT, AFF_ADR, AFF_VAL.
Un codage des listes est nécessaire dans la phase sémantique afin de les ranger dans la table des types et les référencer dans la table des objets.
La sémantique consiste à définir d’une part les quadruplets nécessaires correspondant aux opérations définies sur les listes linéaires chaînées et d’autre part déterminer l’emplacement des fonctions sémantiques dans les règles de grammaire ainsi que leurs description en détail.
18.2 Table des types (TABTYP)
![]()
Nous utilisons le codage suivant:
L pour liste de chaînes de caractères.
W pour la constante NIL
Exemples
Une liste linéaire chaînée de chaînes de caractères est codée en LS.
Une liste de structures simples à trois champs (Entier, Booleen, Car) est codée en L(EBC) .
La sémantique d’une déclaration de liste linéaire chaînée consiste à former le type tel que décrit ci-dessus.
18.3 Quadruplets
![]()
Pour les opérations d’allocation / Libération ALLOUER(P) et LIBERER(P) les quadruplets suivants sont à générer:
- (‘Allouer’,A ,B, C )
A, B non utilisés.
C : pointeur dans TABOB vers le résultat.
- (‘Liberer’, A ,B, C )
A, B non utilisés.
C : pointeur dans TABOB vers le maillon à libérer.
Pour les opérations d’accès VALEUR(Exp) et SUIVANT(Exp) les quadruplets suivants sont à générer:
- (‘Valeur’,A ,B, C )
A : pointeur dans TABOB vers le résultat de Exp.
B non utilisés.
C : pointeur dans TABOB vers le résultat.
- (‘Suivant’,A ,B, C )
A : pointeur dans TABOB vers le résultat de Exp.
B non utilisés.
C : pointeur dans TABOB vers le résultat.
Pour les opérations de mise à jour AFF_ADR(Exp1, Exp2) et AFF_VAL(Exp1, Exp2) les quadruplets suivants sont à générer:
- (‘Aff_val’,A ,B, C )
A : pointeur dans TABOB vers le résultat de Exp1.
B non utilisés.
C : pointeur dans TABOB vers le résultat de Exp2.
- (‘Aff_adr’,A ,B, C )
A : pointeur dans TABOB vers le résultat de Exp1.
B non utilisés.
C : pointeur dans TABOB vers le résultat de Exp2.
18.4 Syntaxe
![]()
Notre grammaire est étendue comme suit avec les règles en surbrillance portant sur les listes linéaires chaînées.
Déclarations
<Algo Z> → [ ~Soit|Soient~ <Ps> ] Debut <Lis> Fin [;] { ~<Act> | <Fonct>~ [;] }*
<Act> → Action Idf [ ( <Li> ) ] [;] [ ~Soit|Soient~ <Ps> ] Debut <Lis> Fin
<Fonct> → Fonction Idf ( <Li> ) : <Typ> [ ~Soit|Soient~ <Ps> ] Debut <Lis> Fin
<Ps> → <S>;{ [~Soit|Soient~] <S>;}*
<S> → <Li> Sep ~ <Typ> | ~Action|Fonction(<Typ>)~ ~
<Li> → Idf {, Idf}*
<Typ> → Types | <Structsimple> | <Structcomplexe> |
Machine_car |
Machine_nombre |
[Pointeur vers [Sep] ] Liste
[ De ~Types | <Structsimple>]~ |
Tableau (<Lc>) [De~<Structsimple> | Types~ ] |
<Structsimple> → [Structure ](Types {, Types }*)
<Structcomplexe> → [Structure ]( ~ Types|Vecteur(Cste) [De Types] ~ {, ~ Types | Vecteur(Cste) [De Types] ~ }*)
<Lc> → Cste {, Cste}*
Instructions:
< Lis > → < Inst > { ; < Inst > }*
<Inst> → Idf := <Exp> |
Lire ( Idf {, Idf }* ) |
Ecrire (<Exp> {,<Exp>}* ) |
Tantque <Exp> [ : ] <Lis> Fintantque |
Si <Exp> [:] <Lis> [Sinon <Lis>] Fsi |
Pour Idf:= <Exp>,<Exp> [, <Exp>][:] <Lis> Finpour |
Appel Idf [(Exp {,<Exp>}*)]
~Liberer| Allouer~ ( <Exp> ) |
~ Aff_adr|Aff_val~ ( <Exp> , <Exp> ) |
~Creer_liste |Init_vecteur|Init_struct|Creer_mnombre~ ( Idf , [[ ~<Exp>|[[<Exp> {, <Exp>}*]] ~ {, ~<Exp>|[[<Exp> {, <Exp>}*]]~}* ]] ) |
Aff_element ( <Exp> [[ <Exp> {, <Exp> }* ]] ,<Exp> ) |
Aff_struct(Idf, Cste, <Exp>) |
Creer_mcar(Idf, [[ Chaine ]]) |
~Lirecar|Lirenombre~ (Idf, Idf)
Expressions:
<Exp> → <Exps>[ Opr <Exps>]
<Exps> → [Sign] <Terme> { Opa <Terme> }*
<Terme> → <Facteur>{Opm <Facteur>}*
<Facteur> → Idf [(Exp {,<Exp>}*)] | Cste | ( <Exp>) | <Fonct> | | Non <Facteur> | Vrai | Faux | Nil | Chaine
<Fonct> → ~Valeur|Suivant~ ( <Fonct> ) |
Element ( <Fonct> [[ <Exp> {, <Exp> }* ]] ) |
Struct ( Idf, Cste) |
~Nbrcar|NbrNombre~ (Idf)
18.5 Fonctions sémantiques
![]()
Déclaration
La sémantique consiste à former le type.
<Typ> → [Pointeur vers [Sep] ] Liste F1[ De ~Types F2 | <Structsimple> F3 ~ ] F4
F1
Type = ‘L’ .
F2
Si Sem = ‘Chaine’ alors Type = Type + ‘S’ sinon Type = Type + Sem[1].
F3
Type = Type + Type_st; Type_st étant le type de <Structsimple>.
F4
Si le dernier caractère de Type est ‘L’ alors rajouter ‘E’ au type Type qui devient ainsi ‘LE’.
Spécification
<S> → <Li> [ Sep <Typ> ] F1
F1
Soit L la liste produite par <Li> et soit Type le type produit par <Typ>.
Ranger Type dans TABTYP s’il n’existe pas. Soit I son indice dans cette table.
Pour chaque Idf dans L :
- Le mettre dans la table des symboles;
- Lui attribuer un type
- Lui attribuer une adresse relative A et le mettre dans la table des objets TABOB (soit Pt son emplacement dans cette table). L’objet créé aura comme Statut=‘L’;Type=I; Nombre=Longueur de Type et Adresse=A;
Allouer et Libérer
<Inst> → ~Liberer F1 | Allouer F2 ~ ( <Exp> ) F3
F1
Sauv = Sem
F2
Soit Temp le résultat de <Exp>. Si Temp n’est pas une liste: Erreur
F3
Générer un temporaire Temp2 du même type que Temp.
Générer le quadruplet (Sauv, , , Temp2).
Aff_adr et Aff_val
<Inst> → ~ Aff_adr F1 |Aff_val F1 ~ ( <Exp> F2 ,<Exp> F3 ) F4
F1
Sauv = Sem.
F2
Soit Temp le résultat de <Exp>.
Si Temp n’est pas une liste: Erreur. Soit Type_L le type des éléments de la liste.
F3
Soit Temp2 le résultat de <Exp>.
Si Temp2 n’est pas de type Type_L: Erreur. Temp2 peut être une constante de Type_L ou NIL. Dans ce cas, la constante est rangée dans TABCONS.
F4
Générer le quadruplet(Sauv, Temp, , Temp2).
Creer_liste
<Inst> → ~ Creer_liste( Idf F1 , [[ ~<Exp> F2 |
[[<Exp> F4 {, <Exp> F5 }*]] ~
{, ~<Exp> F3 |
[[<Exp> F4 {, <Exp> F5 }*]]~}*
]] ) F6
F1
Si Idf n’est pas une liste:Erreur. Soit Type_L le type des éléments de la liste et Ptidf l’emplacement de Idf dans TABOB.
F2
Soit Temp le résultat de <Exp>. Si Temp n’est pas du type Type_L : Erreur.
Nb=1; Mettre Temp dans TABCOMP (table complémentaire). Soit Deb sa position dans cette table.
F3
Soit Temp le résultat de <Exp>.
Si Temp n’est pas du type Type_L: Erreur.
Nb=Nb+1; Mettre Temp dans TABCOMP.
F4
Soit Temp le résultat de <Exp>.
Si Temp n’est pas du premier type de Type_L : Erreur (Ici, Type_L est une structure simple).
Nb=1; Mettre Temp dans TABCOMP (table complémentaire). Soit Deb sa position dans cette table.
F5
Soit Temp le résultat de <Exp>.
Si Temp n’est pas du type correspondant dans Type_L: Erreur. (Ici, Type_L est une structure simple)
Nb=Nb+1; Mettre Temp dans TABCOMP.
F6
Générer le quadruplet(‘Creer_liste, Ptidf, Deb, Nb)
Remarque : Dans F2, F3, F4 et F5, Temp peut être une constante. Dans ce cas, cette dernière est rangée dans la table des constantes(TABCONS) et Temp désigne alors l’indice de l’objet créé dans la table des objets TABOB.
Constante Nil
<Facteur> → Nil F1
F1
Mettre la constante Nil dans la table des constantes TABCONS si elle ne figure pas et retourner son indice dans cette table.
Valeur et Suivant
<Fonct> → ~Valeur F1 | Suivant F1 ~ ( <Fonction> ) F2
F1
Sauv := Sem.
F2
Soit Temp le temporaire contenant le résultat de <Fonction>.
Vérifier que Temp est une liste.
Créer un objet Temp2 du type des éléments de la liste qui recevra à l’exécution le résultat de la fonction.
Générer le quadruplet (Sauv, Temp, , Temp2).
18.6 Exemple1
![]()
La figure 35 montre les tables de compilation créées par la phase sémantique pour le programme source donné.
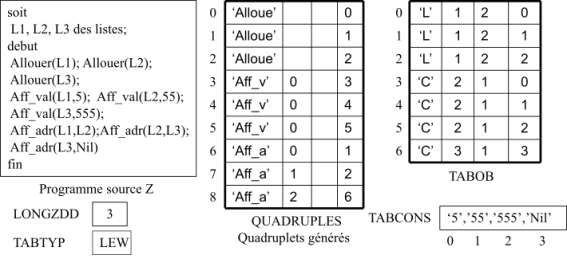
Figure 35: Tables de compilation(Listes linéaires chaînées)
18.7 Exemple2
![]()
La figure 36 montre les tables de compilation créées par la phase sémantique pour le programme source donné. La liste est créée avec l’opération de haut niveau Creer_liste.
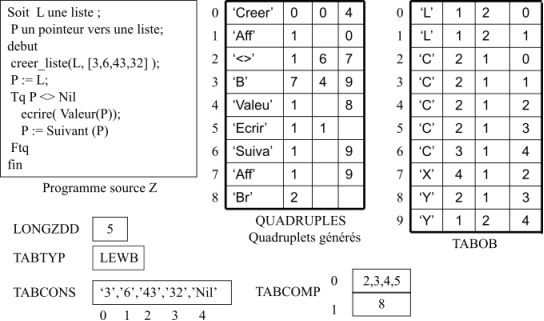
Figure 36: Tables de compilation(Listes linéaires chaînées)
18.8 Interprétation
![]()
L’interprétation des listes linéaires chaînées consiste à définir une représentation mémoire pour un maillon d’une liste et traduire tous les quadruplets dans cette représentation.
Une liste linéaire chaînée peut être définie comme suit (description PASCAL) :
Typeliste = ^Elementliste;
Elementliste = RECORD
Element : POINTER;
Suivant : Typeliste
END;
A la rencontre du quadruplet (‘Allouer’,A ,B, C ) avec les paramètres définis comme suit:
A, B non utilisés.
C : pointeur dans TABOB vers le résultat.
les opérations suivantes sont effectuées:
Soit ZDD le tableau d’adresses représentant la zone de données.
- Allocation d’un maillon du type défini ci-dessus. Soit ADR son adresse.
- Récupérer de TABOB l’adresse relative D dans la zone de données du paramètre C.
- Ranger dans ZDD [ D ] l’adresse ADR.
A la rencontre du quadruplet (‘Valeur’,A ,B, C ) avec les paramètres définis comme suit:
A : pointeur dans TABOB vers le maillon.
B non utilisés.
C : pointeur dans TABOB vers le résultat.
les opérations suivantes sont effectuées:
Soit ZDD le tableau d’adresses représentant la zone de données.
- Récupérer de TABOB l’adresse relative D dans la zone de données du paramètre A. C’est l’adresse du maillon.
- Récupérer de TABOB l’adresse relative D2 dans la zone de données du paramètre C.
- Ranger dans ZDD [ D2 ] le champ ‘Valeur’ du maillon d’adresse D.
A la rencontre du quadruplet (‘Aff_val’,A ,B, C ) avec les paramètres définis comme suit:
A : pointeur dans TABOB vers le maillon.
B non utilisés.
C : pointeur dans TABOB vers le résultat de l’expression à affecter.
les opérations suivantes sont effectuées:
Soit ZDD le tableau d’adresses représentant la zone de données.
- Récupérer de TABOB l’adresse relative D dans la zone de données du paramètre A. C’est l’adresse du maillon.
- Récupérer de TABOB l’adresse relative D2 dans la zone de données du paramètre C.
- Ranger dans le champ ‘Valeur’ du maillon d’adresse D la valeur référencée par ZDD[D2] .