Sommaire                    Définition du langage d’expérimentation          Compilateur pour le langage Z minimal          Extensions du langage Z minimal

Chapitre précédent               Chapitre 14 : Structures simples et tableaux               Chapitre suivant

14.1 Introduction

14.2 Représentation d’un tableau en mémoire

14.3 Représentation d’une structure simple en mémoire

14.4 Rangement d'un tableau à plusieurs dimensions en mémoire

14.5 Adressage des éléments d’un tableau

14.6 Table des types  (TABTYP)

14.7 Table des objets (TABOB )

14.8 Quadruplets

14.9 Syntaxe

14.10 Fonctions sémantiques

14.11 Exemple 1

14.12 Exemple 2

14.13 Interprétation

14.1 Introduction  

Une structure simple est un ensemble d’éléments de types différents. Chaque type est simple (ENTIER, BOOLEEN, CAR, CHAINE). Nous utilisons aussi le terme enregistrement pour désigner une structure simple.

Un tableau est un ensemble d’éléments de même type. Chaque élément peut être de type simple ou de type structure simple.

La sémantique des structures simples et des tableaux revient à donner une solution aux problèmes suivants:

- Comment représenter un tableau en mémoire?

- Comment représenter une structure simple en mémoire?

- Comment représenter un tableau à plusieurs dimensions en mémoire et du coup comment accéder à un élément du tableau?

- Comment coder les tableaux et les structures simple?

- Comment les mettre dans la table des objets?

- quels sont les quadruplets à générer?

- Où insérer les fonctions sémantiques dans les règles?

- Décrire les fonctions sémantiques.

- Comment  seront interpréter les quadruplets générés?

Dans ce qui suit nous donnons des solutions à tous les problèmes posés.

14.2 Représentation d’un tableau en mémoire  

La figure 19 montre comment un tableau est représenté en mémoire pendant l’exécution d’un programme. Au niveau de la zone de données, nous mettons l’adresse vers le descriptif du tableau. Ce dernier contient l’adresse du premier élément du tableau, la dimension du tableau ainsi que les bornes de chaque dimension.

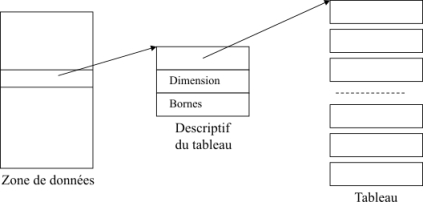
 Figure 19: Représentation d’un tableau en mémoire

14.3 Représentation d’une structure simple en mémoire   

La figure 20 montre comment une structure simple est représentée en mémoire pendant l’exécution d’un programme. Au niveau de la zone de données, nous mettons l’adresse vers le descriptif de la structure. Ce dernier contient les adresses vers les différents champs de la structure

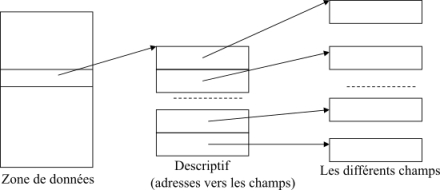
Figure 20: Représentation d’une structure simple en mémoire

14.4 Rangement d'un tableau à plusieurs dimensions en mémoire  

Une déclaration typique d’un tableau à plusieurs dimensions peut être la suivante : A(a₁ :b₁ ; a₂ :b₂ ; ......a_n:b_n)

a₁ et b₁ sont les bornes de la première dimension, a₂ et b₂ sont les bornes de la seconde dimension, etc.

Le tableau est rangé de manière contiguë comme suit:

- On range d’abord le sous tableau  A(a₁ , *, *, ..., *), puis le sous-tableau A(a₁₊₁, *, *, ..., *), et ainsi de suite jusqu’au sous-tableau A(b₁ , *, *, ..., *) .

L’étoile (*) désigne toutes les valeurs possibles pour une dimension.

- A l'intérieur de chaque sous tableau A(i, *, *, ...., *), l'ordre suivant des sous-sous- tableaux est considéré :

A(i, a₂ , *, *, ..., *), A(i, a₂₊₁, *, *, ..., *), A(i, a₂₊₂, *, *, ..., *),  ......, A(i, b₂ , *, *, ..., *)

Et ainsi de suite ...

Donc il s’agit d’un rangement de la matrice ligne par ligne. Ce sont les derniers indices qui varient le plus rapidement.

  Exemple

La figure 21 montre comment le tableau A(1:3, 1:2, 1:3) est représenté en mémoire. Les éléments sont rangés dans l’ordre suivant: A(1, 1, 1), A(1, 1, 2), A(1, 1, 3), A(1, 2, 1), etc.

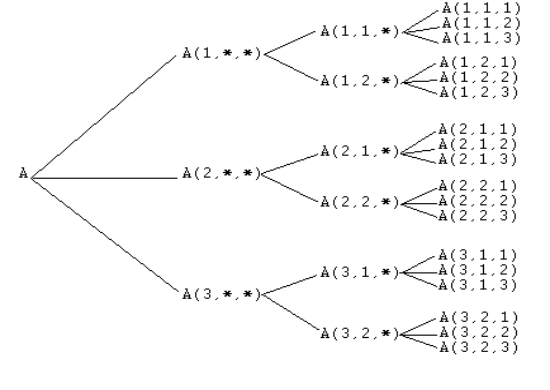
Figure 21: Ordre de rangement d’un tableau en mémoire

14.5 Adressage des éléments d’un tableau  

Une fois que la politique de placement des éléments est fixée, nous voulons maintenons accéder à l’élément A(i₁ , i₂ .., i_n).

Posons d_i = b_i - a_i + 1. C’est le nombre maximal d’éléments dans la dimension i du tableau.

L’adresse de A(i₁ , *, *, ....), notée AD₁ est égale à Base + (i₁ -a1 ) d₂d₃ ...d_n.

Base désigne l’adresse mémoire du premier élément du tableau.

L’adresse de A(i₁ , i₂ , *, ...., *), soit AD₂ est égale à  AD₁ + (i₂ -a₂ )d₃d₄ ...d_n .

Et d’une manière générale, l’adresse de A(i₁ , i₂ , ...i_n ), notée AD_n est égale à

Base + (i₁ -a₁ )d₂d₃ ..d_n + (i₂ -a₂ )d₃d₄ ...d_n + ....+(i_n-1-a_n-1)d_n + (i_n -a_n)

Dans cette formule, il ya une partie constante et une partie variable.

La partie constante est : Base -(a₁ Π_i=2,n d_i+ a₂ Π_i=3,n d_i+...+a_n-1d_n + a_n )

La partie variable est : i₁ Π_i=2,n d_i + i2 Π_i=3,n d_i + ...+ i_n-1d_n + i_n 

Dans le cas où a₁ = a₂ = ...... = a_n = 0, l‘adresse de A(i₁ , i₂ , ...i_n ) est

i₁d₂d₃ ..d_n + i₂d₃d₄ ...d_n + ....+i_n-1d_n + i_n 

Ou bien :

∑_j=1,n ( i_j . Π_i=j+1,n d_i )

d_id_i+1...d_n est appelé facteur multiplicatif.

14.6 Table des types  (TABTYP)  

Une codification est adoptée pour désigner les types. Pour les types standards, nous avons déjà utilisé la codification suivante:

‘E’ Entier

‘B’ Booléen

‘C’ Caractère

‘S’ Chaîne de caractères

Une structure est codée de la manière suivante:

‘(’ , suivi des types de ses champs et de ‘)’.

Exemples

Une structure ayant pour champs un entier, une chaîne de caractères et un booléen est codé en  (ESB).

Un tableau est codé de la manière suivante:

‘T’ ou ‘V’ pour Tableau (ou Vecteur), suivi de ses dimensions séparées par des virgules et du type de ses éléments.

Exemples

Un tableau Tab(4,3) de entiers est codé en T4,3E.

Un tableau Tab(10) de chaînes de caractères est codé en T10S.

Un tableau Tab(5, 10, 20) de structures simples ayant pour champs un entier, une chaîne de caractères et un booléen est codé en T5,10,20(ESB).

De cette manière TABTYP est un tableau de caractères (ou une chaîne de caractères) contenant tous les types.

14.7 Table des objets  (TABOB )  

Nous allons modifier la structure d’une entrée de la table des objets afin de pouvoir généraliser le champ Statut et de référencer la table des types TABTYP via les champs Type et Nombre.

Dans la suite du document, les champs Statut, Type, Nombre et Adresse d’une entrée de la table des objets sont définis comme suit:

- Statut qui peut être :

'L' : Variable locale.

'X' : Variable auxiliaire de valeur créée par le compilateur.

'Y' : Variable auxiliaire d'adresse créée par le compilateur.

'C' : Constante entière, logique , pointeur ou chaîne de caractères.

- Type : Indice vers la tables des types TABTYP .

- Nombre : Longueur du type (nombre de caractères formant le type).

- Adresse : désigne soit l’adresse relative de l'objet dans la zone de données si le statut est 'L', 'X' ou 'Y', soit le rang dans TABCONS si le statut est 'C'.

14.8 Quadruplets  

Nous introduisons deux classes de quadruplets. Ceux correspondant à l’objet tableau et ceux correspondant à l’objet structure.

Pour les structures, au niveau des déclarations (voir grammaire) nous introduisons le quadruplet (‘Ds’, A, B, C ) avec les paramètres A, B et C définis comme suit:

A : pointeur TABOB vers l’objet composé.

B, et C non utilisés.

Pour un objet structure, les champs ont les valeurs suivantes:

Statut=‘L’,

Type= indice dans la table des types (TABTYP),

Nombre=nombre de caractères formant le type,

Adresse=adresse relative de l’objet dans la zone de données.

Quant aux opérations STRUCT(S, Rang), AFF_STRUCT(S, Rang, Exp) et INIT_STRUCT(S,[Exp1, Exp2, …]), les quadruplets suivants sont considérés:

- (‘Struct’, A, B, C )

A : pointeur dans TABOB vers l’objet structure.

B : numéro (ou rang) du champ .

C : pointeur dans TABOB vers le résultat de l’opération STRUCT.

(‘Aff_struct’, A, B, C )

A : pointeur dans TABOB vers l’objet structure.

B : numéro (ou rang)du champ.

C : pointeur dans TABOB vers la valeur à affecter.

- (‘Init_struct’, A, B, C )

A : pointeur dans TABOB vers l’objet structure.

B : pointeur dans TABCOMP vers la liste des expressions scalaires.

C : nombre d’expressions.

Pour les tableaux, au niveau des déclarations (voir grammaire) nous introduisons le quadruplet (‘Dt’, A, B, C ) avec les paramètres A, B et C définis comme suit:

A : pointeur dans TABOB vers l’objet tableau.

B : indice dans TABCOMP vers les bornes des dimensions.

D : dimension.

Pour un objet tableau, les champs ont les valeurs suivantes:

Statut=‘L’,

Type= indice dans la table des types (TABTYP),

Nombre=nombre de caractères formant le type,

Adresse=adresse relative de l’objet dans la zone de données.

Quant aux opérations ELEMENT(T[Exp1, Exp2, .. ]),  AFF_ELEMENT(T[Exp1, Exp2,..], Exp) et  INIT_TABLEAU(T, [[Exp1, Exp2,..]) les quadruplets suivants sont considérés:

- (‘Element’, A, B, C )

A : pointeur TABOB vers l’objet tableau.

B : pointeur dans TABCOMP vers la liste des expressions.

C : pointeur dans TABOB vers le résultat de ELEMENT.

- (‘Init_vect’, A, B, C )

A : pointeur TABOB vers l’objet tableau.

B : pointeur dans TABCOMP vers la liste des expressions.

D : pointeur dans TABOB vers la valeur à affecter.

- (Aff_Element’, A, B, C )

A : pointeur TABOB vers l’objet tableau.

B : pointeur dans TABCOMP vers la listes des expressions.

C : non utilisé

14.9 Syntaxe  

 Notre grammaire courante est augmentée avec les règles relatives aux tableaux et structures simples (en surbrillance) comme suit:

Déclarations

<Algo Z>             →     [ ~Soit|Soient~ <Ps> ] Debut <Lis> Fin [;]

<Ps>                   →     <S>;{ [~Soit|Soient~] <S>;}*

<S>                    →     <Li> Sep <Typ>

<Li>                   →     Idf {, Idf}*

<Typ>                →     Types | <Structsimple> | Tableau (<Lc>) [De~<Structsimple> | Types~ ]

<Structsimple>    →     [Structure ](Types {, Types }*) <Lc> → Cste {, Cste}*

Instructions

< Lis >              →     < Inst > { ; < Inst > }*

<Inst>               →     Idf := <Exp> |

                     Lire ( Idf {, Idf }* ) |

                     Ecrire (<Exp> {,<Exp>}* ) |

                     Tantque <Exp> [ : ] <Lis> Fintantque |

                     Si <Exp> [:] <Lis> [Sinon <Lis>] Fsi |

                     Pour Idf:= <Exp>,<Exp> [, <Exp>][:] <Lis> Finpour

                    ~ Init_vecteur | Init_struct ~  Idf , [[ ~<Exp>|[[<Exp> {, <Exp>}*]] ~   { , ~<Exp>|[[<Exp> {, <Exp>}*]]~}* ]] ) |

                    Aff_element (<Exp> [[ <Exp> {, <Exp> }* ]] ,<Exp> ) |

                    Aff_struct(Idf, Cste, <Exp>)

Expressions

<Exp>             →     <Exps>[ Opr <Exps>]

<Exps>           →     [Sign] <Terme> { Opa <Terme> }*

<Terme>        →     <Facteur>{Opm <Facteur>}*

<Facteur>      →     Idf | Cste | ( <Exp>) | <Fonct> | Non <Facteur> | Vrai | Faux | Chaine

<Fonct>         →     Element ( <Fonct> [[ <Exp> {, <Exp> }* ]] ) | Struct ( Idf, Cste)

14.10 Fonctions sémantiques  

Déclaration de structure

<Typ>     →     [Structure ] (Types F1 {, Types  F2 }* )  F3

La sémantique consiste à former le type de la structure.

F1

Soit Type une variable de type chaîne de caractères. Faire Type=‘(‘+Types.

F2

Faire Type= Type + Types.

F3

Faire Type= Type + ‘)’.

Déclaration de tableau

< Tableau >     →     <Typ>  Tableau  F1 (<Lc>) [De~<Structsimple> | Types~ ]  F4

<Lc>              →     Cste F2 {, Cste F3  }*

La sémantique consiste à former le type du tableau.

F1

Faire Type=‘V‘; Type_element=‘E’ (par défaut’).

F2

Faire Type= Type +Cste; Ranger Cste dans TABCOMP. Soit PtComp l’emplacement dans cette table; Compte:=1.

F3

Faire Type= Type + ‘,’+Cste; Ranger Cste dans TABCOMP puis faire Compte= Compte +1.

F4

Soit T le type produit par <Structsimple> ou Types. Faire Type_element = T; Faire Type= Type + Type_element.

Spécification

<S>         →     <Li> [ Sep <Typ> ]  F1

Déjà traité en P7. A ce niveau, c’est plus général.

F1

Soit L la liste produite par <Li> et soit Type le type produit par <Typ>. Ranger Type dans TABTYP si Type n’existe pas. Soit I son indice dans cette table.

Pour chaque Idf dans L :

- Le mettre dans la table des symboles;

- Lui attribuer une adresse relative A et le mettre dans la table des objets (soit Pt son emplacement). L’objet créé aura comme Statut=‘L’;Type=I; Nombre=Longueur de Type et Adresse=A;

- Si type simple :Générer le quadruplet (‘D’+Type, Pt, , ).

- Si structure simple : Générer le quadruplet (‘Ds’, Pt, , ).

- Si tableau : Générer le quadruplet (‘Dt’, Pt, , ).

 Aff_struct

< Inst>      →     Aff_struct (Idf  F1, Cste  F2 , <Exp>) F3 

F1

Vérifier que Idf est déclarée comme une structure. Sinon Erreur. Soit Pt son emplacement dans TABOB.

F2

Récupérer le nombre N de champs de la structure.

Si Cste <1 ou Cste > N :Erreur.

Récupérer le type T du champ de rang Cste.

F3

Soit Temp le résultat de <Exp>. Vérifier si le type de Temp est égal à T. Si non égal : erreur.

Générer le quadruplet ( ‘Aff_struct’, Pt, Cste, Temp).

Aff_element

< Inst>      →     Aff_element (<Exp>  F1  [[ <Exp> F2 {, <Exp>  F3 }* ]] , <Exp> ) F4

F1

Soit Temp1 (emplacement dans TABOB) le résultat de <Exp> et soit Type son type.

Si Type n’est pas un tableau : Erreur.

Récupérer dans Typtab son type et dans Dim sa dimension.

F2

Soit Temp le résultat de <Exp>.

Si son type n’est pas un entier: Erreur.

Initialiser Compte à 0.

Mettre Temp dans la table TABCOMP. Soit Ptabcomp son emplacement.

F3

Soit Temp le résultat de <Exp>.

Si son type n’est pas un entier: Erreur.

Incrémenter Compte d’une unité.

Mettre Temp dans la table TABCOMP.

F4

Soit Temp2 (emplacement dans TABOB) le résultat de <Exp> et soit Type2 son type.

Si Type2 # Typtab : Erreur. Si Compte # Dim : Erreur.

Générer le quadruplet (‘Aff_element’, Temp1, Ptabcomp, Temp2).

Struct

< Inst>      →     Struct ( <Exp>  F1 , Cste )  F2

F1

Soit Temp1 (emplacement dans TABOB) le résultat de <Exp> et soit Type2 son type.

Si Type2 n’est pas une structure : Erreur.

Récupérer le nombre de champs de la structure dans N et le type du champ de rang Cste de la structure dans Typechamp.

F2

Vérifier que Cste est entière et comprise entre 1 et N. Sinon Erreur.

Générer un temporaire d’adresse avec le Satut=‘Y’et avec Type= Typechamp. Soit Temp2 son emplacement dans TABOB.

Générer le quadruplet (‘Struct’, Temp1, Cste, Temp2).

 Element

< Inst>      →     Element ( <Fonct>  F1 [[ <Exp> F2 {, <Exp>   F3 }* ]] ) F4 

F1

Soit Temp1 (emplacement dans TABOB) le résultat de <Fonct> et soit Type2 son type.

Si Type2 n’est pas un tableau : Erreur.

Récupérer la dimension du tableau dans Dim et le type des éléments dans Typtab.

F2

Soit Temp le résultat de <Exp>.

Vérifier que Temp est du type entier, sinon Erreur.

Intialiser Compte à 0.

Mettre Temp1 dans la table TABCOMP. Soit Ptabcomp son emplacement dans cette table.

F3

Soit Temp le résultat de <Exp>.

Si son type n’est pas un entier: Erreur.

Incrémenter Compte d’une unité.

Mettre Temp dans la table TABCOMP.

F4

Si Dim # Compte : Erreur.

Générer un temporaire d’adresse avec le champ Statut=‘Y’ et avec Type= Typtab. Soit Temp2 son emplacement dans TABOB.

Générer le quadruplet (‘Element’, Temp1, Ptabcomp, Temp2).

Init_Struct et Init_vecteur

< Inst>      →     ~ Init_vecteur F1 | Init_struct  F1 ~ ( Idf  F2 , [[ ~ <Exp>  F3 | [[<Exp> F5 {, <Exp>  F6 }*]] ~ {, ~ <Exp> F4 |        

                         [[<Exp>  F5 {, <Exp>  F6  }* ]]~ }* ]] )  F7

F1

Sauv = Sem, Sem étant l’unité lexicale reconnue.

F2

Si Idf n’est pas un tableau ou une structure selon Sauv: Erreur. Soit Ptidf l’emplacement de Idf dans TABOB et Type le type des éléments du tableau ou de la structure.

F3

Soit Temp le résultat de <Exp>.

Si Temp n’est pas du type Type : Erreur.

Nb=1; Mettre Temp dans TABCOMP (table complémentaire). Soit Deb sa position dans TABCOMP.

F4

Soit Temp le résultat de <Exp>.

Si Temp n’est pas du type Type: Erreur.

Nb=Nb+1; Mettre Temp dans TABCOMP.

F5

Soit Temp le résultat de <Exp>.

Si Temp n’est pas du premier type de Type : Erreur (Ici, Type est une structure simple).

Nb=1; Mettre Temp dans TABCOMP (table complémentaire). Soit Deb sa position dans cette table.

F6

Soit Temp le résultat de <Exp>.

Si Temp n’est pas du type correspondant dans Type: Erreur. (Ici, Type est une structure simple)

Nb=Nb+1; Mettre Temp dans TABCOMP.

F7 

Générer le quadruplet(Sauv, Ptidf, Deb, Nb).

14.11 Exemple 1  

Les figures 22 et 23 montrent les tables de compilation pour les programmes source donnés. La table des objets TABOB est remplie selon les nouvelles conventions considérées dans cette section. Noter aussi la présence de la table des types TABTYP.

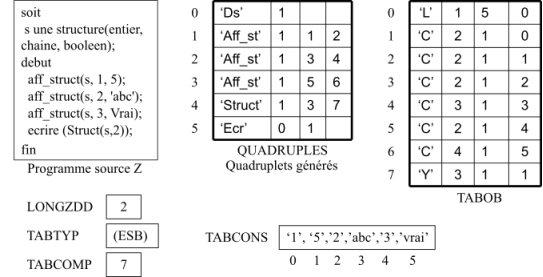
Figure 22: Tables de compilation(Structures)

14.12 Exemple 2  

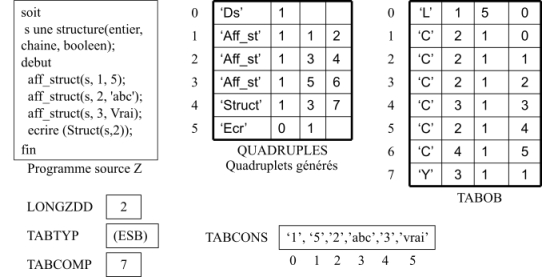
Figure 23: Tables de compilation(Tableaux)

14.13 Interprétation  

L’interprétation consiste à exécuter un code pour chaque type de quadruplet. Ce code peut être exprimé dans un langage de programmation quelconque.

À la rencontre du quadruplet (‘Dt’, Pt, Liste , Dim ) avec la signification suivante de ses paramètres:

Pt : pointeur dans TABOB vers l’objet tableau.

Liste : pointeur dans TABCOMP vers la liste des bornes.

Dim : dimension (nombre de bornes).

Le code avec les opérations suivantes est exécuté:

- Allocation d’une zone pour le descriptif et son remplissage.

- Mettre l’adresse de ce descriptif dans la zone de données.

- Allocation d’un espace pour le tableau et initialisation à Nil.

À la rencontre du quadruplet  (‘Ds’, Pt, , ) avec la signification suivante de son paramètre Pt:

Pt : pointeur dans TABOB vers la structure.

Il y a

- Allocation d’un espace pour le descriptif de la structure dont la taille est égale au nombre de champs.

-  Mettre l’adresse de ce descriptif dans la zone de données.

- Allocation pour les différents champs en fonction des types.

À la rencontre du quadruplet (‘Element’, Ptobj, Ptcomp , Ptres ) avec la signification suivante de ses paramètres:

Ptobj : pointeur dans TABOB vers le tableau.

Ptcom : pointeur dans TABCOMP.

Ptres : pointeur vers l’objet où sera rangé le résultat.

Les opérations suivantes sont entreprises :

- Accès au descriptif via le champ Adresse de Ptobj. On y trouvera l’adresse du premier élément du tableau.

- Utiliser le module de calcul d’adresse pour calculer l’emplacement de l ’élément d’indices i1, i2, i3, ..

(Ces indices sont récupérés grace à Ptcom via TABCOMP et TABOB )

- Vérifier que les indices sont bien dans les intervalles permises, Sinon Erreur.

- Récupérer le résultat dans Ptres.

À la rencontre du quadruplet (‘Struct’, Ptobj, Ptcons , Ptres ) avec la signification suivante de ses paramètres:

Ptobj : pointeur dans TABOB vers la structure.

Ptcons : pointeur dans TABOB vers la constante (numéro du champ).

Ptres : pointeur vers l’objet où sera rangé le résultat.

Les opérations suivantes sont entreprises :

- Accès à la structure via le champ Adresse de Ptobj. On y trouvera l’adresse

du premier élément de la structure.

- Vérifier que la constante référencée par Ptcons est dans l’intervalle. Sinon Erreur.

- Récupérer le résultat dans Ptres.

À la rencontre du quadruplet (‘Aff_struct’, Ptobj, Ptcons , Ptobj2 ) avec la signification suivante de ses paramètres:

Ptobj : pointeur dans TABOB vers la structure.

Ptcons : pointeur dans TABOB vers la constante (numéro du champ)

Ptobj : pointeur vers l’objet qui contient le résultat à affecter au champ concerné.

Les opérations suivantes sont entreprises :

- Accès à la structure via le champ Adresse de Ptobj. On y trouvera l’adresse du premier élément de la structure.

- Vérifier que la constante référencée par Ptcons est dans l’intervalle. Sinon Erreur.

- Affecter au champ référencé par Ptcons, le contenu de la valeur référencée par Ptobj2.

À la rencontre du quadruplet  (‘Aff_element’, Ptobj, Ptobj2 , Ptobj3 ) avec la signification suivante de ses paramètres:

Ptobj : pointeur dans TABOB vers le tableau.

Ptobj2 : pointeur dans TABCOMP vers l’objet contenant le premier indice du tableau.

Ptobj3 : pointeur vers l’objet qui contient le résultat à affecter.

Les opérations suivantes sont entreprises :

- Accès au descriptif via le champ Adresse de Ptobj. On y trouvera l’adresse du premier élément du tableau.

- Utiliser le module de calcul d’adresse pour calculer l’emplacement E de l ’élément d’indice i1, i2, i3, ..

(Ces indices sont récupérés grace à Ptobj2 via TABCOMP et TABOB).

Vérifier que les indices sont bien dans les intervalles permises, Sinon Erreur.

- Ranger à l’emplacement E la valeur référencée par Ptobj3.

À la rencontre du quadruplet (‘Init_vect’, Ptobj, Ptobj2 , Ptobj3 ) avec la signification suivante de ses paramètres:

Ptobj : pointeur dans TABOB vers le tableau.

Ptobj2 : pointeur dans TABCOMP vers l’objet contenant le premier élément à affecter.

Ptobj3 : pointeur vers l’objet qui contient le nombre d’éléments à affecter.

Les opérations suivantes sont entreprises :

- Accès au descriptif via le champ Adresse de Ptobj. On y trouvera l’adresse du premier élément du tableau.

- Récupérer le nombre d’éléments à copier via Ptobj3.

- Copier les valeurs des objets référencés dans la table complémentaire TABCOMP à partir du rang Ptobj2 dans le tableau.

À la rencontre du quadruplet (‘Init_struct’, Ptobj, Ptobj2 , Ptobj3 ) avec la signification suivante de ses paramètres:

Ptobj : pointeur dans TABOB vers la structure.

Ptobj2 : pointeur dans TABCOMP vers l’objet contenant le premier élément à affecter.

Ptobj3 : pointeur vers l’objet qui contient le nombre d’éléments à affecter.

Les opérations suivantes sont entreprises :

- Accès à la structure via le champ Adresse de Ptobj. On y trouvera l’adresse du premier élément de la structure.

- Récupérer le nombre d’éléments à copier via Ptobj3.

- Copier les valeurs des objets référencés dans la table complémentaire TABCOMP à partir du rang Ptobj2 dans la structure.