Sommaire Définition du langage d’expérimentation Compilateur pour le langage Z minimal Extensions du langage Z minimal
Chapitre précédent Chapitre 13 : Structures de contrôle Chapitre suivant
13.4.1 Boucle ‘Tantque’
13.4.2 Exemple ( Boucle ‘Tantque’)
13.4.3 Boucle ‘Pour’
13.4.4 Exemple (Boucle ‘Pour’)
13.4.5 Conditionnelle ‘Si-Sinon’
13.4.6 Exemple (Conditionnelle ‘Si-Sinon’)
13.1 Objectif
![]()
Il s’agit de traduire les structures de contrôle TANTQUE, POUR et SI-SINON en opérations de bas niveau avec uniquement les branchements conditionnels et inconditionnels.
13.2 Quadruplets
![]()
Rappelons qu’une instruction de branchement conditionnel est définie comme suit:
‘Si Exp Aller à Et1 Sinon Aller à Et2 Fsi’
et qu’une instruction de branchement inconditionnel est définie comme suit:
‘Aller à Et1’
Deux types de quadruplets sont alors utilisés.
- Quadruplet relatif au branchement conditionnel : (‘B’, B, C , D ) avec les paramètres décrits comme suit:
B : pointeur dans TABOB vers le résultat de Exp.
C : Et1 (pointeur dans la table des quadruplets: QUADRUPLES).
D : Et2 (pointeur dans QUADRUPLES)
- Quadruplet relatif au branchement inconditionnel : (‘Br’, B, C , D ) avec les paramètres décrits comme suit:
B : Et1 (pointeur dans QUADRUPLES).
C et D non utilisés.
13.3 Syntaxe
![]()
Considérons le langage Z minimal augmenté des règles relatives aux structures de contrôle (en surbrillance) au sein de sa grammaire.
Déclarations
<Algo Z> → [ ~Soit|Soient~ <Ps> ] Debut <Lis> Fin [;]
<Ps> → <S>;{ [~Soit|Soient~] <S>;}*
<S> → <Li> Sep <Typ>
<Li> → Idf {, Idf}*
<Typ> → Entier | Booleen | Chaine | Car
Instructions
< Lis > → < Inst > { ; < Inst > }*
<Inst> → Idf := <Exp> |
Lire ( Idf {, Idf }* ) | Ecrire (<Exp> {,<Exp>}* ) |
Tantque <Exp> [ : ] <Lis> Fintantque |
Si <Exp> [:] <Lis> [Sinon <Lis>] Fsi |
Pour Idf:= <Exp>,<Exp> [, <Exp>][:] <Lis> Finpour
Expressions
<Exp> → <Exps>[ Opr <Exps>]
<Exps> → [Sign] <Terme> { Opa <Terme> }*
<Terme> → <Facteur>{Opm <Facteur>}*
<Facteur> → Idf | Cste | ( <Exp>) | Non <Facteur> | Vrai | Faux | Chaine
Pour les trois structures de contrôle, nous montrons ci-après où insérer les fonctions sémantiques dans les règles de grammaire ainsi que leurs descriptions en détail.
13.4 Fonctions sémantiques
![]()
13.4.1 Boucle ‘Tantque’
<Inst> → Tantque F1 <Exp> [ : ] <Lis> F2 Fintantque F3
F1
Soit Ptquad le pointeur du dernier quadruplet généré.
Sauvegarder Ptquad +1 dans Sauv.
F2
Soit Temp le résultat de <Exp> (emplacement dans TABOB). Si son type n’est pas booléen : Erreur.
Générer le quadruplet (‘B’, Temp, Ptquad+2, X ).
Sauvegarder son emplacement dans Sauv2.
F3
Générer le quadruplet (‘Br’, Sauv, , ).
Remplacer X par Ptquad + 1 dans le quadruplet Sauv2.
13.4.2 Exemple ( Boucle ‘Tantque’)
La figure 16 montre dans QUADRUPLES les quadruplets générés pour la boucle Tantque figurant dans le programme source donné.
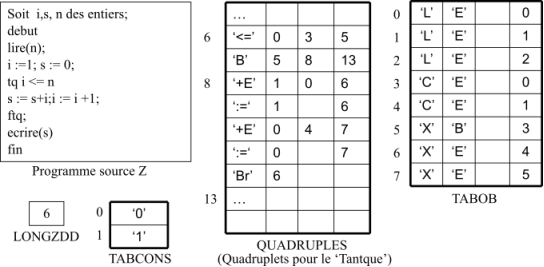
Figure 16: Tables de compilation (Boucle Tantque)
13.4.3 Boucle ‘Pour’
<Inst> → Pour Idf F1 := <Exp> F2 ,<Exp> F3 [,<Exp> F4 ][:] F5 <Lis> Finpour F6
F1
Si Idf n’est pas déclaré : Erreur.
Si le type de Idf n’est pas entier : Erreur.
Soit Ptidf son pointeur dans TABOB.
F2
Soit Temp le résultat de <Exp> (emplacement dans TABOB).
Si son type n’est pas entier : Erreur.
Générer le quadruplet (‘:=’, Ptidf, , Temp ).
F3
Soit Temp2 le résultat de <Exp> (emplacement dans TABOB).
Si son type n’est pas entier : Erreur.
F4
Soit Temp3 le résultat de <Exp> (emplacement dans TABOB).
Si son type n’est pas entier : Erreur.
F5
- Cas où le pas existe : créer la constante ‘0’; soit Ptcons son emplacement dans TABOB.
Générer un temporaire booléen; soit Tb son emplacement dans TABOB.
Générer le quadruplet (‘<‘, Temp3, Ptcons, Tb).
Sauvegarder sa position dans QUADRUPLES dans Sauv.
Générer le quadruplet (‘B’, Tb, Ptquad+2, Ptquad+4).
Générer un autre temporaire booléen; soit Tb2 son emplacement dans TABOB.
Générer le quadruplet (‘>=‘, Ptidf, Temp2, Tb2).
Générer le quadruplet (‘Br’, Ptquad+3, , ).
Générer le quadruplet (‘<=‘, Ptidf, Temp2, Tb2).
Générer le quadruplet(‘B’,Tb2, Ptquad + 2, X).
Sauvegarder son emplacement dans QUADRUPLES dans Sauv2.
F6
- Cas où le pas existe : Générer le quadruplet (‘+E‘, Ptidf, Temp3, Ptidf).
- Générer le quadruplet(‘Br’, Sauv, ,).
Remplacer X par Ptquad + 1 dans le quadruplet Sauv2.
13.4.4 Exemple (Boucle ‘Pour’)
La figure 17 montre dans QUADRUPLES les quadruplets générés pour la boucle Pour figurant dans le programme source donné.
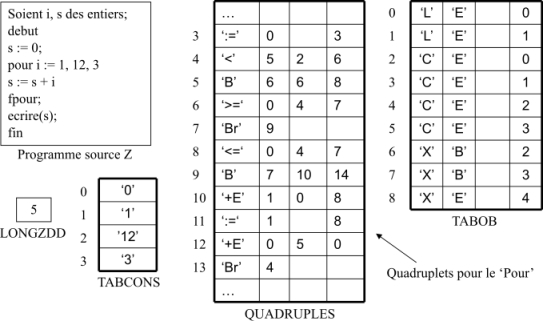
Figure 17: Tables de compilation (Boucle Pour)
En fin de compilation le programme source est remplacé par les tables QUADRUPLES, TABOB, TABCONS et LONGZDD.
13.4.5 Conditionnelle ‘Si-Sinon’
<Inst> → Si <Exp> [:] F1 <Lis> [Sinon F2 <Lis>] Fsi F3
F1
Soit Temp le résultat de <Exp> (emplacement dans TABOB).
Si son type n’est pas booléen : Erreur.
Générer le quadruplet (‘B’, Temp, Ptquad+2, X).
Sauvegarder son emplacement dans Sauv.
F2
Générer le quadruplet (‘Br’, Y, ,).
Sauvegarder son pointeur dans Sauv2.
Remplacer X par Ptquad + 1 dans le quadruplet Sauv.
F3
Cas où la partie ‘Sinon’ existe : Remplacer Y par Ptquad + 1 dans le quadruplet Sauv2.
Cas où la partie ‘Sinon’ n’existe pas : Remplacer X par Ptquad + 1 dans le quadruplet d’emplacement Sauv.
13.4.6 Exemple (Conditionnelle ‘Si-Sinon’)
La figure 18 montre dans QUADRUPLES les quadruplets générés pour l’alternative Si-Sinon figurant dans le programme source donné.
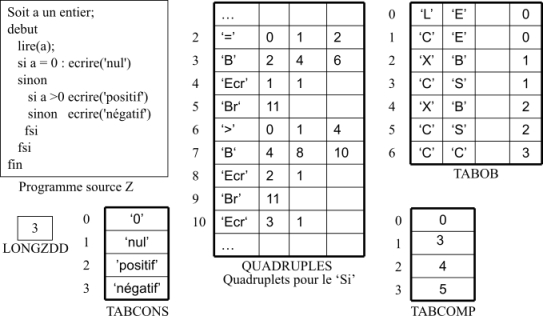
Figure 18: Tables de compilation (Alternative Si-Sinon)