Exercices
1. Montrer
que le parcours récursif préordre dans un arbre binaire est linéaire (O(n)), n
étant le nombre total de nœuds.
Rappel : Pr(A) = SI A ( NIL : Ecrire(Info(A)); Pr(Fg(A)); Pr(Fd(A)) FSI
2. Expliquer pourquoi des méthodes de recherche donnant la solution optimale telles que 'Branch and Bound' et 'l'algorithme A*' sont classées parmi les recherches Heuristiques ?
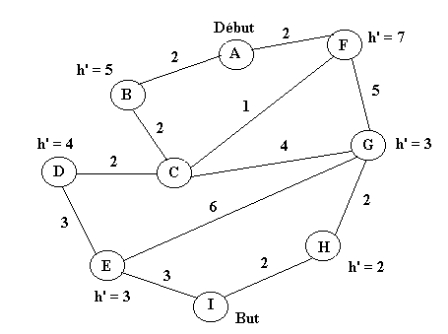
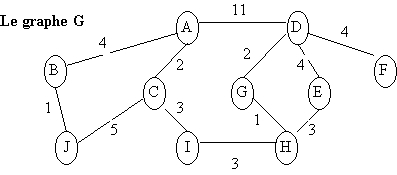
3. Soit G un graphe représentant un espace de recherche donné. L’état initial est le nœud A et l’état solution est le nœud H. T* est une fonction d’estimation du trajet restant vers le nœud solution :

x T*(x)
A 2
B 5
C 5
D 3
E 3
F 7
G 4
H 0
I 3
J 2
Quelles sont
les méthodes de recherches permettant de générer les solutions :
a) A-C-I-H b) A-D-G-H c) A-D-E-H
4..Trouver
la complexité de la fonction suivante :
FONCTION conv(n,b :entier) : entier
SI n
£ b :
conv ¬ n ;
SINON
X
¬ conv(
n div b, b ) ;
conv
¬ X
* 10 + n mod b ;
FSI
5. Donner
la solution trouvée par la méthode ‘Branch and Bound avec programmation
dynamique’ en montrant les chemins abandonnés par la programmation dynamique
durant le processus de recherche du chemin entre les nœuds ‘A’ et ‘K’ dans le
graphe représenté par la matrice des coûts suivante :
|
|
A |
B |
C |
D |
E |
F |
G |
H |
I |
J |
K |
|
A |
|
3 |
4 |
1 |
|
|
|
|
|
|
|
|
B |
3 |
|
|
3 |
4 |
|
|
|
|
|
|
|
C |
4 |
|
|
|
|
3 |
3 |
|
|
|
|
|
D |
1 |
3 |
|
|
|
1 |
|
|
4 |
|
|
|
E |
|
4 |
|
|
|
|
|
|
|
2 |
|
|
F |
|
|
3 |
1 |
|
|
|
|
|
|
|
|
G |
|
|
3 |
|
|
|
|
1 |
|
|
|
|
H |
|
|
|
|
|
|
1 |
|
|
5 |
2 |
|
I |
|
|
|
4 |
|
|
|
|
|
1 |
|
|
J |
|
|
|
|
2 |
|
|
5 |
1 |
|
3 |
|
K |
|
|
|
|
|
|
|
2 |
|
3 |
|
NB : En cas d’égalité de valeurs de la fonction d’estimation, le choix des
successeurs se fera suivant l’ordre alphabétique.
6. Donner
la complexité des programmes suivants :
a) i := n;
j := 1;
TQ i > 0
SI i = 1
j := j + 4;
SI j < n i := n FSI
FSI
i := i – 1
FTQ
b) P( a, b, c )
SI a = 0
c := b
SINON
x = 0; i := 1
TQ i < a
P( a div 2, b-1, c );
x := x+c;
i := i * 2
FTQ;
c := x
FSI
7. Un
tri topologique des sommets d'un graphe orienté sans circuit G, consiste à
construire une liste L de tous les sommets de G, de telle sorte que s'il existe
un arc (i,j) dans G, alors i précède j dans la liste résultat L. Donner un
algorithme basé sur le parcours en profondeur, qui construit une telle liste.
8.
Soit la fonction Constr(i,j), qui construit un arbre binaire équilibré à partir
d'un tableau ordonné T de n éléments :
Constr( i, j : entier ) : pointeur
Var R, R1, R2 : pointeur;
m : entier;
SI (i > j) R := NIL
SINON
SI (i = j)
R:= CreerNoeud(T[i])
SINON
m := (i+j) div 2;
R1 := Constr(i, m-1);
R2 := Constr(m+1, j);
R := CreerNoeud( T[i] ); Aff-fg( R, R1 ); Aff-fd( R, R2 );
FSI
FSI;
Constr := R;
Donner la complexité de la fonction Constr sachant que les opérations
CreerNoeud, Aff-fg et Aff-fd sont élémentaire ( o(1) ).
9.
Donner la complexité de la procédure suivante :
Chemins(n, k : entier; var L : matrice[n,n])
SI (k=0)
POUR i:=1, n
POUR j:=1, n
L[i,j] := D[i,j]
FPOUR
FPOUR
SINON
Chemin(n, k-1, M);
POUR i:=1, n
POUR j:=1, n
L[i,j] := min( M[i,j], M[i,k]+M[k,j] )
FPOUR
FPOUR
FSI
10.
Soient deux algorithmes A et B ayant une complexité de O(log n) et O(n0.1)
respectivement. Comparer les deux complexités.
11. Calculer
la complexité de l'algorithme suivant:
i : = 1;
a := 0;
TQ i*i < n
a := a+i;
i := i * 3
FTQ
12.
Soit G = (S,A) un graphe non orienté et connexe (c-a-d il existe une chaîne
(chemin) entre chaque couple de sommets). Les arêtes sont valuées par des poids.
On cherche à former un sous graphe connexe et sans cycle (arbre recouvrant)
ayant un poids total minimal.
Donner un algorithme de type glouton (ou vorace) qui détermine un tel arbre.
13. Donner la complexité de l'algorithme suivant:
x := a; y := b;
TQ (x <= y)
x := x+1; y := y-1
FTQ
14.
Mesurer l'efficacité dans le pire des cas, des programmes (P et Q) suivants :
P : x = n ;
y = 1 ;
TQ ( x > 1 )
z = m*1000000 ;
TQ ( z > 1 )
y = y + n * (x – z ) ;
z = z - 10
FTQ
y = y - x ;
x = x / 2
FTQ
Q : F(x,y,z)
SI ( x >= z )
Retourner y+z
SINON
Retourner F( x, x+1, z-1 ) + y
FSI
15.
Résolution de problèmes
Donner un algorithme, utilisant un parcours en profondeur, qui affiche toutes
les séquences de longueur n, des éléments d'un ensemble de taille n. Quelle est
sa complexité.
Exemple : Soit l'ensemble E = {a, b, c}, alors toutes les séquences de longueur
3 sont :
abc, acb, bac, bca, cab et cba.
16. Soient
M la matrice des coûts d'un graphe G et H la fonction d'estimation du coût
restant.
- Quel est le chemin trouvé par l'algorithme A* du nœud A vers le nœud F.
- Quels sont les chemins abandonnés (par programmation dynamique) au cours du
processus de recherche.
- Discuter la qualité du chemin trouvé.
M
|
|
A |
B |
C |
D |
E |
F |
|
A |
|
4 |
2 |
|
|
|
|
B |
4 |
|
3 |
2 |
|
1 |
|
C |
2 |
3 |
|
1 |
4 |
|
|
D |
|
2 |
1 |
|
2 |
3 |
|
E |
|
|
4 |
2 |
|
|
|
F |
|
1 |
|
3 |
|
|
H
|
A |
B |
C |
D |
E |
F |
|
4 |
3 |
1 |
1 |
2 |
0 |
17. Calculer
la complexité du programme suivant :
P ¬ 1 ;
Pour I = 1 , n
J ¬ 1 ; K ¬ 1 ;
TQ K <= n
P:=P * (K + J) ; K := K + 1 ;
SI K > n : J
:= J + 1 ;
SI J <=
n : K :=1 FSI
FSI
FTQ
FPour
18. Calculer
la complexité de la fonction récursive suivante :
Fonc ( X , Y , Z : Entier ) : Entier ;
Var K , P , S : Entier ;
P := 0 ; S:=1 ;
Pour K =1 , Y
P :=P + K ;
FPour;
Pour K = X , (X + (2*P)div(Y+1) - 1)
S :=S + Fonc ( X div 2 , Y - 1 , Z - 2 ) ;
FPour ;
Fonc := S
19.Donner
la complexité de la procédure B :
B( n : entier; var R : entier )
SI (n = 0)
R := 1;
SINON
SI (n mod 2 = 0)
B( n-2, R ); R := 2*R;
SINON
R := 1; k := n;
TQ (k > 1)
R := 2*R;
k := k – 2;
FTQ
FSI
FSI
20. Trouvez
la complexité de l'algorithme suivant :
F(n:entier) : entier
SI ( n = 0 )
Retourner 1
SINON
i ← 1 ; s ← 0 ;
TQ ( i ≤ n )
s ← s + F(n-1) ; i ← i + 1
FTQ ;
Retourner s*n
FSI
21. Un
véhicule doit se déplacer d'une ville A à une ville B en empruntant une route
sur laquelle existe n stations-service {S1,
S2 …
Sn}.
On connait les distances di séparant
les différentes stations ainsi que le nombre de kilomètres M que peut parcourir
le véhicule avec un plein de carburant.
Ainsi di représente
le nombre de kilomètres séparant la station Si de
la station Si+1,
avec 1 ≤ i < n
d0 représente
la distance séparant la ville A de la première station S1.
dn représente
la distance séparant la dernière station Sn de
la ville B.
- Donnez un algorithme glouton (vorace) qui détermine la plus petite liste de
stations-service où le véhicule doit s'arrêter pour faire le plein de carburant
et atteindre la ville B. On supposera que le véhicule démarre de A avec un
plein de carburant déjà effectué.
- Démontrer que l'algorithme glouton donne la solution optimale pour ce
problème.
22. Dans
l'algorithme A* comment pourrait-on combiner deux fonctions heuristiques (de
sous-estimation) h1 et h2 pour un problème donné, et produire une nouvelle
fonction h de sous-estimation meilleure que h1 et h2.
23.
Calculer la complexité de l'algorithme suivant :
I := n
S := 0
Tq i > 0
J := 2*i
Tq j > 1
S := S + (j-i) * (S+1)
J := j - 1
Ftq
I := i Div 2
Ftq
24. Donner
les arbres de recherche générés par les méthodes
a. Hill Climbing ( Recherche en profondeur avec fonction d’estimation = h )
b. A* ( fonction d’estimation = g + h )
Pour le problème du labyrinthe suivant :
Le robot doit se déplacer de la case R (Position 4,1 ) à la case A (Position 3, 4). Les déplacements en diagonale sont interdits.
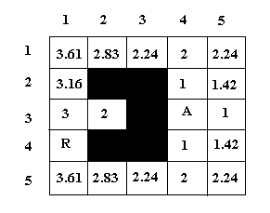
NB : h désigne l’estimation de la distance restante et g le coût du trajet antérieur parcouru.
25.Donner
la complexité de la procédure m(x,y,Z) suivante :
m(x,y :entier ; var Z :entier)
SI y = 0 : Z := 0
SINON SI (y mod 2 = 0): m(x*2, y div 2, Z) SINON m(x*2, y div 2, Z) ; Z
:=Z+x FSI
FSI
26. Trouver
la complexité des algorithmes suivants (justifier vos réponses):
(a)
(b)
i := 1 ; f ( i, j, k :entier) : entier
TQ i < n var x : entier
j := 1 ; SI k+j = i
TQ j < 2*n f := ((i-j) div k) + 1 ;
j := j*2 ; SINON
FTQ x := f(i, j+1, k-2) ;
i := i+1 ; f := f(i+1, j+x, k-2) ;
FTQ FSI
27. Soit G un graphe orienté représentant l’espace de recherche d’un problème donné. M étant la matrice des coûts (M[i,j] est la valeur de l’arc i®j) et H une fonction d’estimation
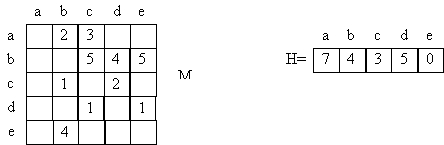
L’état initial et l’état final sont représentés respectivement par les nœuds ‘a’ et ‘e’ :
a) Appliquer ‘Best First Search’ pour donner la liste des nœuds visités (suivant l’ordre de leur exploration et en expliquant le déroulement). (BFS = Largeur + estimation)
b) Même question dans le cas d’une recherche de type ‘Hill Climbing’. (Profondeur + estimation)
c) Donner le chemin généré par la méthode ‘Branch and Bound pure’.(sans estim. et sans prog. dyn.)
d) Donner le chemin généré par A*. (avec estimation et programmation dynamique)
Pour ces deux dernières questions (c et d) expliquer le déroulement et discuter la qualité de la solution trouvée (optimale ou pas et pourquoi ).
28.
Calculer la complexité de la fonction récursive suivante :
Fonc ( X , Y , Z : Entier ) : Entier ;
Var K , P , S : Entier ;
P:= 0 ; S:= 1 ;
Pour K =1 , Y
P:= P + K ;
FPour;
Pour K = X , (X + (2*P)div(Y+1) - 1)
S := S + Fonc ( X div 2 , Y - 1 , Z - 2 ) ;
FPour ;
Fonc (S)
29. Soit
G un graphe représentant l'espace de recherche d'un problème donné et soit M sa
matrice des coûts. On utilise la fonction H comme estimation du coût restant.
- Quel est le chemin trouvé par l'algorithme A* du nœud A vers le nœud F.
- Quels sont les chemins abandonnés (par programmation dynamique) au cours du
processus de recherche.
- Discuter la qualité du chemin trouvé.
M
|
|
A |
B |
C |
D |
E |
F |
|
A |
|
4 |
2 |
|
|
|
|
B |
4 |
|
3 |
2 |
|
1 |
|
C |
2 |
3 |
|
1 |
4 |
|
|
D |
|
2 |
1 |
|
2 |
3 |
|
E |
|
|
4 |
2 |
|
|
|
F |
|
1 |
|
3 |
|
|
H
|
A |
B |
C |
D |
E |
F |
|
4 |
3 |
1 |
1 |
2 |
0 |
30. Trouver
la complexité du programme suivant :
i := 1 ; j := 1 ;
TQ i < n :
SI j < n :
j := j * 2
SINON
j := 1 ; i := i + 1
FSI
FTQ
31.
Soit F(x,n,r) la
procédure récursive suivante:
F( x, n : entier ; var r:entier ) // x et n des entrées et r
une sortie
Si ( n = 0 ) r ← 1
Sinon
F( x , n div 2 , r ) ;
r ← r * r ;
Si ( (n mod 2) = 1 )
r ← x * r
Fsi
Fsi
Donnez la complexité de cet algorithme.
32. Le schéma suivant représente un arbre de recherche d’un jeu donné entre 2 joueurs.
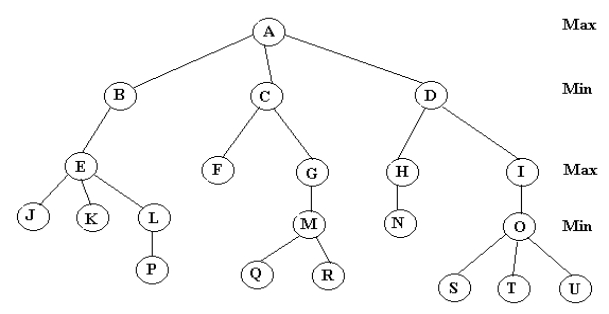
Les feuilles de l’arbre sont évaluées comme suit J : -15, k :12, P :10, F :12, Q :40, R :-40, N :2, S :-20, T :0, U :40
a. Evaluer à l’aide de la procédure Min-Max tous les nœuds de l’arbre.
b. Même chose avec l’élagage alpha-béta, en montrant sur l’arbre les coupes et leur type.
33.
Soit le problème d’optimisation suivant :
« Minimiser le nombre de pièces de monnaie pour totaliser une certaine somme d’argent M »
Ce problème peut être formulé comme suit :
Étant donné des pièces de monnaie ayant des valeurs dans {v1, v2, …. vn}.
Il s’agit de
trouver des entiers naturels xi minimisant
![]() et
tels que
et
tels que ![]() avec
M un nombre entier naturel donné.
avec
M un nombre entier naturel donné.
- Dans le but de résoudre ce problème par la programmation dynamique, il est demandé de trouver une décomposition récursive permettant de calculer le terme C( k , S ) représentant le nombre minimal de pièces pour totaliser exactement le montant S en utilisant seulement des pièces de valeurs v1, v2,...,vk.
- Quel est le problème de l’approche récursive pour le calcul de C( k , S ) ?
34. Donner l’arbre généré par une recherche A* pour le problème du taquin en spécifiant pour chaque nœud la valeur de la fonction d’estimation f= g + h avec
G : longueur du chemin (nombre de transitions ) de la racine au nœud courant
H : nombre de pièces (jetons) mal placés.
Rappel du jeu de taquin :
Il s’agit d’une grille de 3 X 3 contenant 8 jetons numérotés de 1 à 8 et un emplacement libre (case vide). Tout jeton adjacent à la case vide, peut y être déplacé, rendant son emplacement initial libre. Les déplacements peuvent se faire soit horizontalement soit verticalement. A l’état initial, les jetons sont disposés de façon aléatoire dans la grille, et il s’agira de trouver un chemin, s’il existe, menant vers l’état but où les jetons sont rangés suivant un ordre donné. La transition d’un état à un autre se fait par déplacement d’un jeton .

35. Utiliser la technique Min-Max pour évaluer le coût de la racine de l’arbre suivant en indiquant les différentes coupes de branches à faire ( La racine A se trouve sur un niveau maximisant )
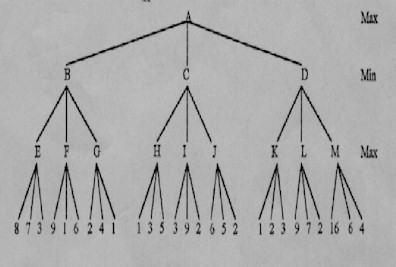
36.
Trouver la complexité de la fonction suivante :
fonction Traitement(x1,y1,x2,y2 : entier) : entier
Si x1=x2
Traitement := M[x1,y1]
Sinon
x12 := (x1 + x2) div 2;
y12 := (y1 + y2) div 2;
T1 := Traitement (x1,y1, x12,y12) * Traitement (x12,y12, x2,y2);
T2 := Traitement (x1,y12, x12,y2) * Traitement (x12,y1, x2,y12);
Traitement := T1 - T2
Fsi
avec M une matrice carré de taille une puissance de 2
37.
Calculer la complexité de la fonction récursive F(x, y, z) suivante :
y := 2*z
Si x > x/(y - z) :
x := x - 2; y := y / 4; z := z / 5;
F(x, y, z);
Fsi
38.
Donnez la complexité de la procédure P suivante:
P(x,y,z) : Si (x = 0) z ← y Sinon P(x-1, y-1, z) ; z ← 2*x-y+z ; P(z-1,
x-y, z) Fsi
39.
Questions de cours (Justifiez vos réponses):
a) Quel est le rôle de l'élagage Alpha-Bêta dans la procédure Min-Max ?
b) Peut-on avoir une solution récursive avec la programmation dynamique ?
40.
Donner la complexité de l’algorithme du parcours Préordre défini sur un arbre binaire :
Pr(n) : Si n <> nil : Ecrire(info(n)) ; Pr(fg(n)) ; Pr(fd(n)) Fsi
41.
En utilisant la technique des équations différentielles, résoudre l’équation de récurrence
T(n) = 3T(n/2) + an, a est une constante.
42.
Soit à résoudre un puzzle composé de 8 carrés numérotés de 1 à 8 placés dans une matrice 3X3. Il existe ainsi une position libre vers laquelle peut se déplacer tout carré adjacent. Le but du problème est de placer les carrés dans la position
1 2 3
4 5 6
7 8
en partant de la situation
1 3
4 2 5
7 8 6
Donner les arbres générés par les méthodes suivantes (en indiquant l’ordre d’exploration des nœuds avec éventuellement une valeur d’estimation pour chaque nœud) :
a) Backtracking b) Hill Climbing c) Branch and Bound
On prendra comme estimation le nombre de carrés bien placés.
43.
Expliquez pourquoi la programmation dynamique est-elle qualifiée de « méthode ascendante » ?
44.
Quand est-ce que l'exploration d'un espace de recherche nécessite t-elle un parcours en largeur ?
45.
Calculez la
complexité de l'algorithme suivant :
i ← 1 ; j ← n
TQ (i < j)
i ← i+1 ;
Si ( i = j ) j
← j div 2 ; i ← 1 Fsi
FTQ
46.
Qu'est-ce
que le principe d'optimalité en programmation dynamique ?
47.
Quelles sont les
différences et les similitudes entre les méthodes de recherche 'Best First
Search' et 'Branch & Bound' ?
48.
Lors de l'évaluation Min-Max d'une configuration J dans un jeu donné, obtient-on les mêmes valeurs avec ou sans élagage Alpha-Bêta ?
49.
Donnez l'arbre
représentant l'espace de recherche exploré par A* pour le problème du taquin.
L'état initial et l'état solution sont comme suit :
1 2 3
1 2 3
6 4
→ 8
4
8 7 5
7 6 5
La fonction d'estimation représente le nombre de pièces mal placées.
50.
Quel type de
parcours (en profondeur ou en largeur) est effectué par 'Branch and Bound' ?
51.
Pourquoi a t-on besoin, généralement, d'une fonction d'estimation d'une configuration dans la procédure Min-Max avec ou sans élagage Alpha-Bêta ?
52.
On veut passer du nombre 15 au nombre 4 en utilisant uniquement les fonctions : f(x) = 3x et g(x) = x div 2
Donnez l’espace de recherche généré par Best First Search, ainsi que l’ordre des visites des différents états, si on utilise la fonction d’estimation h(e) = |e - 4|
53.
Donner la complexité de l'algorithme suivant :
Fonction Bêta (a,b,c,d : entier) : entier;
Si
a>b: .
a :=
b; b:= b-d
Fsi
Si c
> 0:
Bêta(a-l, b+d, c-2, d div 2):
b :=
b-d-1
Fsi
54.
Donner les arbres de recherche générés par
a) Best First Search
b) A*
Pour le graphe des états ci-dessous. Les étiquettes sur les arcs désignent les coûts de transition et h’ représente une fonction d’estimation de proximité d’une solution.