Enoncé 7 : Hachage interne   Corrigé 7

Problème : Hachage virtuel linéaire

Soit une table T(0..M-1) de M cases, Chaque case peut renfermer B données. Initialement, seulement la sous-table T(0..N-1) de N cases primaires (N << M) est réservée aux données, c'est a dire toute donnée D est rangée par la fonction de hachage H_L (D) = D mod (2L.N) avec L = 0. La méthode augmente l'espace des adresses progressivement par l'éclatement des cases dans un ordre prédéfini : d'abord la case 0, puis la case 1,...N-1. Un pointeur P garde la trace de la prochaine case à éclater. l'éclatement d'une case implique le partage ( par la fonction h_L+1) de ses données avec une nouvelle case ajoutée à la fin de la sous-table T(0..N-1). Quand les N cases ont été éclatées et donc le nombre de cases devient égal à 2N, P est remis à 0 et le processus d'éclatement est recommencé de nouveau avec la même fonction H mais avec L incrémenté d'une unité c'est à dire égal à 1. A ce moment, P variera de 0 à 2N-1, doublant ainsi la taille à 4N. Etc.

L'éclatement d'une case est provoqué quand le facteur de chargement & devient supérieur à un seuil S donné. Par conséquent, si on tente d'insérer une donnée D dans une case C alors que celle-ci est pleine, D sera rangée dans une case allouée dynamiquement qui sera chaînée à la case C. Pour chaque case primaire, on peut avoir une liste linéaire chaînée de cases secondaires.

Quand une donnée est supprimée, la contraction sera faite quand & devient inférieur ou égal à un seuil S' donné. C'est l'opération inverse de l'éclatement.

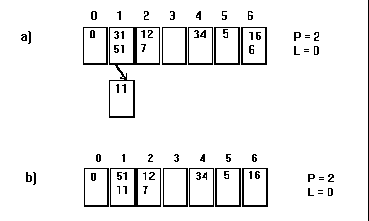
La figure suivante illustre la technique avec les paramètres suivants :

N=5 ; B= 2; S=60%; S'=50%.

a) après insertion des clés : 11, 0, 5, 6, 16, 31, 34, 51, 12, 7

b) après suppression de 6, 31

1. Définir la structure de données et les paramètres de la méthode.

2. Ecrire le module d'initialisation.

3. Ecrire l'algorithme T de transformation donnée-adresse.

4. Utiliser T pour écrire l'algorithme R de recherche d'une donnée D.

5. Utiliser R pour retrouver l'algorithme I d'insertion d'une donnée D.

6. Etudier l'algorithme S de suppression.

- Définir les modules nécessaires sans les écrire en précisant clairement les paramètres d'entrée et de sortie.

- Donner une expression formelle de S en utilisant ces modules.

Remarques:

1. &=nombre de données insérées / ( nombre de cases utilisées X / b)

2. Utiliser les mêmes variables définies dans l'énoncé.

3. I et S sont à concevoir de façon modulaire. Pour chaque module on définira clairement les entrées et les sorties.

4. Lors de l'éclatement, il est préférable de construire une liste linéaire chaînée des données avant de les partager par la nouvelle fonction H_L+1.

5. Une case n'a de suivant que si elle est pleine. Par conséquent, la suppression ne doit pas engendrer des "trous".