Enoncé 34. Arbres  Corrigé 34

Problème : Arbres de recherche binaire en niveaux

Soit à ranger des mots de longueur quelconque dans une structure d'arbre représenté en niveaux comme suit : Chaque nœud p de l'arbre du niveau i à la structure suivante:

(Fg, Ci, Arbre de niveau i+1, Fd)

Tous les caractères rangés dans le sous arbre de racine Fg(p) sont strictement inférieurs à Ci,

Tous les caractères rangés dans le sous arbre de racine Fd(p) sont strictement supérieurs à Ci,

Un mot de la forme : C1 C2 ... Cn sera rangé comme suit :

C1 dans l’arbre de niveau 1

C2 dans un arbre de niveau 2 pointé par le nœud C1

...

Ci dans un arbre de niveau i pointé par le nœud Ci-1

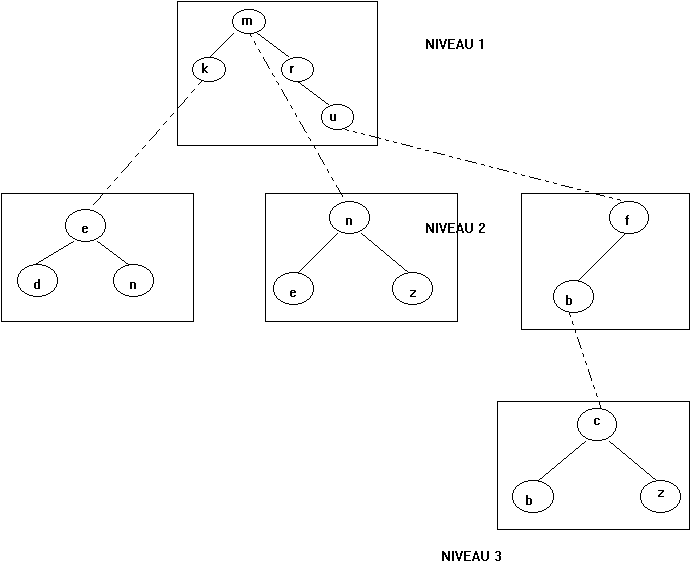
Exemple : Après insertion des mots : mn, ke, me, r, uf, kn, ub, mz, kd, ubc, ubz, ubb nous obtenons l'arbre suivant :

Recherche et insertion dans un arbre de recherche binaire :

Ecrire les algorithmes récursifs suivants de recherche et d'insertion dans un arbre de recherche binaire :

- Rechercher(A, x) : recherche d'un caractère x dans un arbre de racine A. Retourne l'adresse du nœud, Nil sinon.

- Insérer( x, A, B ) : insertion d'un caractère x dans un arbre de racine A. Retourne la racine A et l'adresse B du nœud créé.

Utiliser ces modules pour développer les algorithmes suivants:

Recherche du préfixe : Déterminer le plus grand préfixe (de longueur maximale) dans la structure d'arbre S, d'un mot donné. (Exemple si mot ='ubt', le plus grand préfixe qui existe dans la structure est 'ub')

On écrira le module Préfixe(Mot, Longueur, Adresse) qui retourne la longueur du préfixe et l'adresse du dernier caractère du préfixe dans la structure.

Requête exacte : Déduire le module de recherche d'un mot donné à partir de la recherche du préfixe.

Expansion : Utiliser les modules Préfixe et Insérer pour Insérer un mot donné dans la structure S.

Encombrement : Déterminer l'encombrement (espace) de la structure sachant qu'un pointeur occupe 2 octets.

Programmation : Traduire le module Insérer(x, A, B) ci-dessus en PASCAL.

N.B. Un mot est un tableau de caractères. Long(mot) donne sa longueur en nombre de caractères.

On utilisera le modèle défini sur les arbres de recherche binaire étendu des opérations suivantes :

Arbre(p) : donne l'adresse de l'arbre du prochain niveau

Aff-arbre(p, q) : affecte dans le champ Arbre, l'adresse d'un arbre de racine q)

* * * * *