Corrigé 5.  Enoncé

1. Définition de fonctions récursives

Fonction Trouve ( L, N)

Détermine si un élément N peut être retrouvé dans une liste linéaire chaînée L.
L est un pointeur, N est objet de type quelconque.

    SI L = NIL
        Trouve := FAUX
    SINON
        SI Valeur(L) = N
            Trouve:= VRAI
        SINON    
            Trouve := Trouve( Reste(L), N)
        FSI
    FSI

Fonction Commun (L1, L2)

Détermine si 2 listes linéaires L1 et L2 ont au moins 1 élément en commun.
L1 et L2 sont deux pointeurs de tête de liste :

    SI L1 = NIL
        Commun := FAUX
    SINON
        SI Trouve(L2, Valeur(L1) )
            Commun := VRAI
        SINON
            Commun := Commun ( Reste(L1), L2) )
        FSI
    FSI

Fonction Tous( L1, L2)

Détermine si tous les éléments de L1 peuvent être retrouvés dans L2.
L1 et L2 sont deux pointeurs de tête de liste.

    SI L1 = NIL
        Tous := VRAI
    SINON
        SI NON Trouve(L2, Valeur(L1) )
            Tous := FAUX
        SINON
            Tous := Tous( Reste(L1), L2))
        FSI
    FSI

2. Puzzle

Ecriture de la procédure Construire ( Objet, Arbre1, Arbre2, Arbre )
Objet est un élément de type quelconque.
Arbre1, Arbre2 et Arbre sont des références de type Typearbre ( à définir selon la représentation choisie).
Le corps est le suivant :

    Arbre := Créernoeud( Objet)
    Aff_Fg(Arbre, Arbre1)
    Aff_Fd(Arbre, Arbre2)

Fonction Insérer (X, A)

X est un objet de type quelconque et A est de type Typearbre ( à définir selon la représentation choisie).
Le texte en souligné complète l'algorithme de l'énoncé.

    SI A = NIL
        Construire ( X, NIL, NIL, Arbre)
        Inserer := Arbre
    SINON
        SI X < Info(A)
            Construire(Info(A), Inserer(X, Fg(A)), Fd(A), Arbre)
            Inserer := Arbre ; Liberernoeud(A)
        SINON
            Construire (Info(A), Fg(A),     Inserer(X,Fd(A)), Arbre)
            Inserer := Arbre ; Liberernoeud(A)
        FSI
    FSI

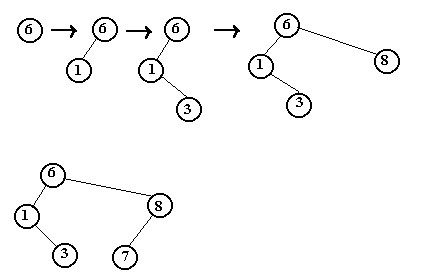
Trace :

3. Représentation séquentielle

    Structures de données
    A est un tableau d'éléments. Chaque élément est le couple(Valeur, Bit).
    TYPE Typecouple = STRUCTURE
        Valeur : Typeqq
        Bit    : BOOLEEN { Présence ou non de l'élément }
    FIN
    L'arbre A est alors défini comme suit ( la racine est toujours à la première position) :
   
    VAR A : Tableau[1..N] DE Typecouple
   
    Implémentation des opérations possibles

    Fg(P) : Fg := 2*p
    Fd(P) : Fd := 2*p + 1
   
Aff_Fg et Aff_Fd n'ont plus de sens ici puisque les champs Fd et Fg n'existent pas dans cette représentation.

    Info(P)                    : Info := A(P).Valeur
    Aff_Info(P, Val)    : A(P).Valeur := Val
    Bit(P)                      : Bit := A(P).Bit
    Aff_Bit(P, B)         : A(P).Bit := B
    Libérer (P)             : A(P).Bit := FAUX

La procédure Créerarbre(A) (créer un arbre vide) suivante est nécessaire pour tout traitement sur des arbres représentés ainsi    :

    POUR I =1,N :    A(I).Bit := FAUX FINPOUR

Algorithme non récursif d'insertion d'un élément X dans un arbre de recherche binaire ainsi représenté

Soit Arbre la racine de l'arbre.

    Lire(X)
    Trouv := FAUX
    P, Q := Arbre
    TANTQUE Q <= N ET Bit(Q) ET NON Trouv (1)
        P := Q
        SI X = Info(P)
            Trouv := VRAI
        SINON
            SI X < Info(P)
                Q := Fg(P)
            SINON
                Q := Fd(P)
            FSI
        FSI
    FINTANTQUE

    SI Trouv
        " X existe déjà"
    SINON
        SI X < Info(P)
            Créeràgauche(P, X)
        SINON
            Créeràdroite(P,X)
        FSI
    FSI

avec Créeràgauche (P, X) définie comme suit :
Soit Q une variable entière.

    Q := Fg(P)
    SI Q > N
        " Erreur "
    SINON    
        SI Bit(Q)
            " Erreur "
        SINON
            Aff_Info(Q, X)
            Aff_Bit(Q, VRAI)
        FSI
    FSI

La procédure Creéràdroite est similaire. Il suffit de remplacer Fg par Fd.

Remarque : dans cet algorithme, Bit(P) est définie comme suit :


    Bit(P) :

    SI P <= N
        Bit := A(p).Bit
    SINON
        Bit := FAUX
    FSI

Sans ça, Bit(Q) ne serait pas définie dans tous les cas dans le critère d'arrêt (1).