Corrigé 4.  Enoncé

1. Différence de deux listes linéaires chaînées

Soit le prédicat Exist(Val, L) égal à VRAI si l'élément Val appartient à la liste L, FAUX Sinon. Soit S le type d'un maillon.
Le prédicat Exist peut être défini comme suit :

    Exist := FAUX
    P := L
    TANTQUE P <> NIL ET NON Exist :
        SI Valeur(P) = Val
            Exist := VRAI
        SINON P := Suivant(P) FSI
    FINTANTQUE

Différence de 2 listes

L'algorithme qui construit la différence de deux listes L1 et L2 est le suivant ( L3 constitue la liste résultante) :

    L3 := NIL
    P := L1
    Q := NIL
    TANTQUE P <> NIL :
        SI NON Exist( Valeur(P), L2)
            R := Q
            Allouer ( Q,S)
            Aff_Val( Q, Valeur(P) )
            Aff_Adr(Q, NIL)
            SI R <> NIL
                Aff_Adr(R,Q)
            SINON L3 := Q FSI
        FSI
        P := Suivant (P)
    FINTANTQUE

2. Files d'attente en représentation contigu�

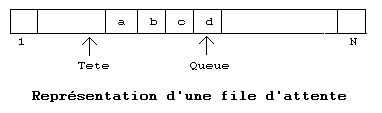
La file d'attente est représentée par un tableau géré de façon circulaire. Tête est l'indice de l'élément qui précède le premier. Queue pointe le dernier élément de la file d'attente. La file d'attente est schématisée comme suit :

Structure de données

    TYPE Typefiledattente = STRUCTURE
        Tab          : TABLEAU(1..N) DE Typeqq
        Tête, Queue     : ENTIER
        Vide          : BOOLEEN
    FIN

Traduction des opérations du modèle dans cette représentation

Créerfile (F)     :     F.Tête, F.Queue := N {Ou n'importe quelle valeur dans [1..N]}
                                 F.Vide := VRAI            

Filevide(F)    :        Filevide := (F.Tête = F.Queue) ET F.Vide
Filepleine(F) :        Filepleine := (F.Tête = F.Queue) ET NON F.Vide
   
Enfiler( F, Val) :    SI NON Filepleine (F)
                                    F.Queue := F.Queue Mod N + 1
                                    F.Tab( F.Queue) := Val
                                    SI F.Queue = F.Tête : F.Vide := FAUX FSI
                               SINON " Overflow " FSI
   
Défiler(F, Val) :    SI NON Filevide(F)
                                    F.Tête := F.Tête Mod N + 1
                                    Val := F.Tab (F.Tête)
                                    SI F.Tête = F.Queue : F.Vide := VRAI FSI
                                SINON " Underflow " FSI

3. Implémentation de file/ pile de piles/files d'attente.

File d'attente de piles

Un schéma possible peut être le suivant :

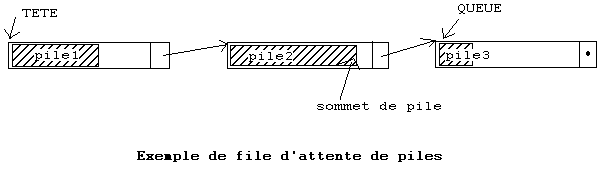
Explication :
La file d'attente est implémentée par une liste linéaire chaînée. Elle est donc définie par le couple(Tête, Queue). Chaque élément de cette liste est une pile représentée en contigu. On a donc une file d'attente de piles.

Structures de données :
    { Pile en représentation statique }
    TYPE Typepile = STRUCTURE
        Tab : TABLEAU (1..N) DE Typeqq
        Sommet : ENTIER
    FIN
    { Un maillon de la file d'attente }
    TYPE S = STRUCTURE
        Pile     : Typepile
        Suivant : POINTEUR(S)
    FIN

    {File d'attente en représentation dynamique}
    TYPE Typefiledattente = STRUCTURE
        Tête, Queue : POINTEUR(S)
    FIN

Les opérations sont traduites comme suit :
F est une variable de type Typefiledattente; Val est une variable de type Typepile.

Créerfile(F)              :      F.Tête := NIL
Filevide(F)                :       Filevide := (F.Tête = NIL)

Enfiler(F, Val)         :      Allouer (Q, S)
                                          Aff_Adr(Q,NIL)
                                          Aff_Val(Q, Val)
                                          SI NON Filevide (F)
                                              Aff_Adr(F.Queue, Q)
                                          SINON F.Tête := Q FSI
                                          F.Queue := Q

Défiler (F, Val)       :      SI NON Filevide(F)
                                              R := F.Tête
                                             Val := Valeur(F.Tête)
                                               F.Tête := Suivant(F.Tête)
                                               Libérer(R)
                                         SINON " Underflow " FSI


Pile de piles

Un schéma possible

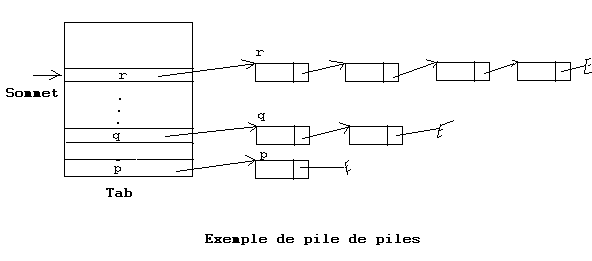
Explication :
La pile principale est implémentée par un tableau. Chaque élément de ce tableau est un pointeur. Ce dernier désigne une pile implémentée par une liste linéaire chaînée. On a donc une pile de piles.

Structures de données :

    { Un maillon de la pile secondaire }
    TYPE S = STRUCTURE
        Element : Typeqq
        Suivant : POINTEUR(S)
    FIN

    {Pile principale en représentation contigue }
    TYPE Typepile = STRUCTURE
        Tab          : TABLEAU(1..N) DE POINTEUR(S)
        Sommet     : ENTIER
    FIN

Pile de files d'attente

Un schéma possible :

Explication :
La file d'attente est implémentée par une liste linéaire chaînée, donc définie par le couple ( Tête, Queue). La pile est implémentée par un tableau o� chaque élément est un couple caractérisant une file d'attente. On a donc bien une pile de files d'attente.

Structures de données :
    { Un maillon de la file d'attente }
    TYPE S = STRUCTURE
        Element : Typeqq
        Suivant : POINTEUR(S)
    FIN
    { File d'attente en représentation dynamique }
    TYPE Typefiledattente = STRUCTURE
        Tête, Queue : POINTEUR(S)
    FIN
    { Pile en représentation statique }
    TYPE Typepile = STRUCTURE
        Tab          : TABLEAU(1..N) DE Typefiledattente
        Sommet     : ENTIER
    FIN