 |
Des méthodes d'index aux méthodes d'arbres
Des méthodes d'index aux méthodes d'arbres
Oublions l'index
secondaire et revenons à l'index primaire. Si le fichier est très volumineux, on ne peut
garder l'index en RAM. De plus, garder l'index en mémoire secondaire coûte cher car :
1) la recherche dichotomique exige beaucoup d'accès disque.
2) il faut maintenir
l'index ordonné (pour pouvoir faire la recherche dichotomique).
Nous devons donc trouver une meilleure façon de faire les insertions et les suppressions d'articles avec seulement une réorganisation locale.
Arbre de recherche binaire comme solution
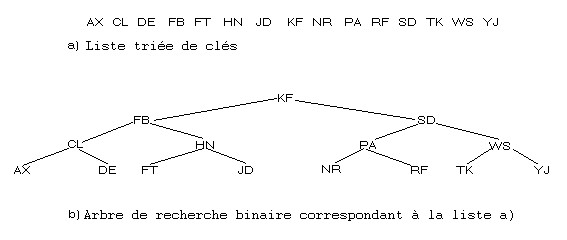
Etant donnée une liste triée de nombres, on peut construire un arbre de recherche binaire comme le montre la figure suivante :
 |
L'arbre peut être représenté dans un tableau comme suit :
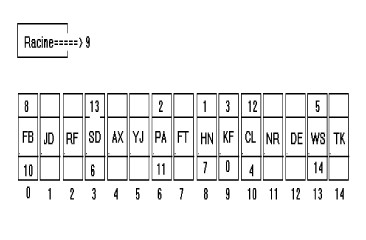 |
Avec cette structure on a pas besoin de trier l'index pour pratiquer la recherche binaire. Donc, c'est une solution pour le point 2).
Cette représentation
admet les deux inconvénients suivants :
a) Plus de
la moitié des liens ne sont pas utilisés car se sont des noeuds feuilles. Ceci entraîne
la perte d'un
espace
considérable.
b) Les performances de recherche sont très mauvaises si l'arbre est
déséquilibré. Pour maintenir l'arbre
équilibré, on
utilise les techniques d'arbre AVL que nous développerons par la suite.
Il faut aussi noter que la structure de l'arbre dépend de l'ordre d'arrivée des clés. Si l'arbre est équilibré on a de bonnes performances de recherche. Quand les clés arrivent de façon aléatoire, l'arbre peut se déséquilibrer et donc les performances se détériorent.
Si on ajoute à l'arbre
précédent les clés : NP , MB, TM, LA, UF, ND, TS, NK
L'arbre devient :
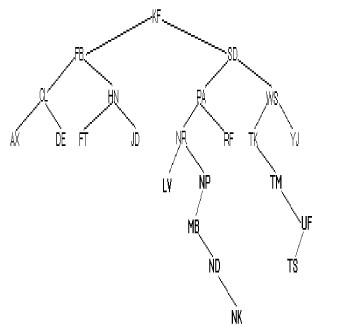 |
Pour certaines clés, on peut avoir 5, 6 ou plusieurs accès avant de les retrouver. Une solution consiste à maintenir l'arbre équilibré. Un arbre maintenu équilibré est appelé arbres AVL (G.M Adel'son-Velskii et E.M Landis). Les arbres AVL garantissent les performances de la recherche et approchent celles de l'arbre binaire complet. Le maintien d'un arbre sous sa forme AVL implique l'application de 4 sortes de rotations. La plus complexe exige la modification de 5 liens (Voir chapitre suivant).
Revenons aux deux
problèmes cités au début :
1) recherche binaire exige plusieurs accès disque.
2) garder l'index ordonné coûte cher.
Les arbres AVL apportent une solution au point 2.
Regardons le point 1) : une solution consiste à paginer l'arbre.
Pagination de l'arbre
ça consiste à organiser l'arbre en pages. Chaque page contient une portion de l'arbre de recherche binaire. Les pages sont rangées dans des blocs sur le disque. L'organisation est alors la suivante :
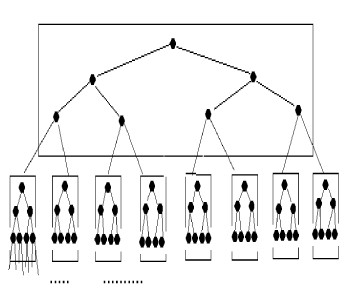 |
Si on prend une page(bloc) de 8K-octets, ce qui permet d'avoir à peu près 511 (clés,
références), et si on suppose que chaque page contient un arbre binaire complet alors
avec 3 accès on peut retrouver un article parmi 511 X 511 X 511 = 134 217 727.
Si on veut éviter la perte d'espace au détriment du temps on peut garder l'arbre de recherche binaire sous sa forme séquentielle "inordre". Ca revient donc à la structure de tableau. Par exemple, l'arbre suivant:
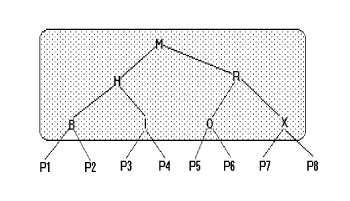 |
peut se mettre sous la forme du tableau suivant : (p1, B, p2, H, p3, I, p4, M, p5, O, p6, P, p7, X, p8)
![]() Si une clé est insérée on procède par décalage, ce qui n'est pas grave car la page est entièrement en mémoire.
Si une clé est insérée on procède par décalage, ce qui n'est pas grave car la page est entièrement en mémoire.
![]() Si l'arbre de recherche binaire n'est pas découpé en pages on a LOG2 (N + 1) accès au maximum.
Si l'arbre de recherche binaire n'est pas découpé en pages on a LOG2 (N + 1) accès au maximum.
![]() Si l'arbre est découpé en pages à raison de k clés par page, on a LOG k+1 (N+1).
Si l'arbre est découpé en pages à raison de k clés par page, on a LOG k+1 (N+1).
Le premier cas est un cas particulier du deuxième avec k=1( une clé par page).
Pour l'exemple
précédent on :
LOG2(134 217 727) =
27 accès
LOG511+1(134 217 727) = 3 accès.
Donc c'est une solution pour le point 1).
On aboutit à ce qu'on appelle un arbre de recherche m-aire. C'est donc un arbre de recherche binaire découpé en pages.
Définitions
Techniques d'équilibrage
Algorithme d'insertion
Analyse théorique
Exemple d'insertions de données dans un arbre AVL
Un arbre binaire équilibré (ou arbre AVL) est un arbre dans lequel les profondeurs des deux sous arbres de chaque noeud ne diffèrent pas plus d'un. A chaque noeud est associé un facteur d'équilibrage qui est égal à la différence entre la profondeur du sous arbre gauche et celle du sous arbre droit. Dans la figure suivante, la profondeur de chaque noeud est placée dans le noeud.
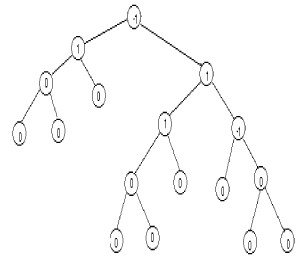 |
Quand on insère un élément, l'arbre peut devenir non équilibré. La figure qui suit illustre tous les cas possibles d'insertions. Les ui désignent les cas o?l'arbre se déséquilibre.
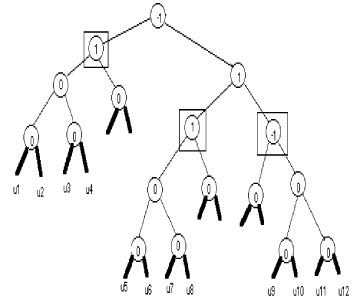 |
Il est facile de voir que
l'arbre devient non équilibré quand le nouveau noeud inséré :
- est un descendant gauche d'un noeud qui avait
un facteur d'équilibrage égal à 1 (u1 à u8)
- est un descendant droit d'un noeud qui avait
un facteur d'équilibrage égal à -1(u9 à u12).
Le plus jeune antécédent qui devient non équilibré est représenté dans un carré.
Examinons un sous arbre de racine le plus jeune antécédent qui devient non équilibré suite à une insertion. Prenons le cas o?le facteur d'équilibrage est 1 pour ce jeune antécédent. La figure suivante illustre ce cas.
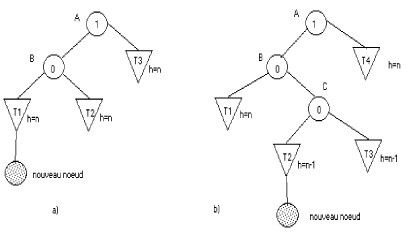 |
A désigne le plus jeune antécédent devenu non équilibré. Puisque f(A)=1, son sous arbre gauche est non NIL. Soit donc B le fils gauche. f(B) doit donc avoir la valeur 0. Ce noeud B devait avoir avant l'insertion des sous arbres (droit et gauche) la même profondeur, soit h=n. Puisque f(A)=1, le sous arbre de A doit aussi avoir h=n.
![]() Deux cas sont à considérer figure a) et b) :
Deux cas sont à considérer figure a) et b) :
Dans a), le nouveau noeud est inséré dans le sous arbre gauche de B. Donc f(B) devient 1 et f(A) devient 2.
Dans b), le nouveau noeud est inséré dans le sous arbre droit de B. f(B) devient -1 et f(A) devient 2.
Afin de maintenir l'arbre
binaire équilibré, il est nécessaire de transformer l'arbre de telle sorte que :
(i) -l'inordre soit préservé.
(ii) -l'arbre transformé soit équilibré.
1. Si une rotation droite est faite sur le sous arbre de racine A dans la figure a), on obtient l'arbre a) suivant qui respecte (i) et (ii).
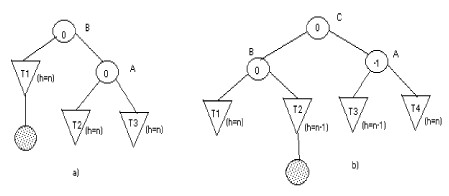 |
2. Considérons la figure b) dans laquelle
le nouveau noeud est inséré dans le sous arbre droit de B. Soit C le fils droit de B.
Trois cas peuvent se présenter:
- C est le nouveau noeud créé.
- le noeud créé est dans le sous gauche de C.
- le noeud créé est dans le sous arbre droit de C.
La figure b) illustre le cas o?le nouveau noeud est dans le sous arbre gauche de C. Si on fait une rotation gauche du sous arbre de racine B suivie par une rotation droite du sous arbre de racine A on obtient l'arbre b) qui respecte (i) et(ii).
Le raisonnement est le même pour le cas o?le facteur d'équilibrage est -1.
La première partie de
l'algorithme consiste à insérer la clé dans l'arbre sans tenir compte du facteur
d'équilibrage. Elle garde aussi la trace du plus jeune antécédent, soit Y qui devient
non équilibré. La deuxième partie fait la transformation à partir de Y.
On démontre que la profondeur maximale d'un arbre binaire équilibré est 1.44*Log2n. La recherche dans un tel arbre n'exige jamais plus de 44% de plus de comparaisons que pour un arbre binaire complet. Pour n grand, l'arbre de recherche binaire équilibré se comporte bien avec un temps de recherche égal Log2(n) + 0.25. En moyenne une rotation est faite pour 46.5% des insertions.
En guise de conclusion de cette section, nous illustrons, ci-après, le mécanisme de construction.
Exemple d'insertions de données dans un arbre AVL
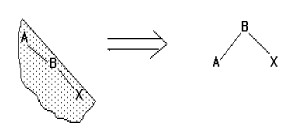
Insérons la séquence : A, B, X, L, M, C, D, E, H, R, S, F dans un arbre AVL.
Insertion A, B, X
 |
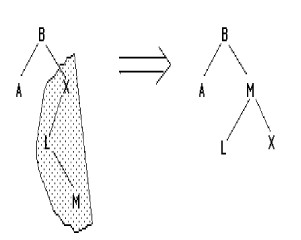
Insertion de L, M
 |
Insertion de C
 |
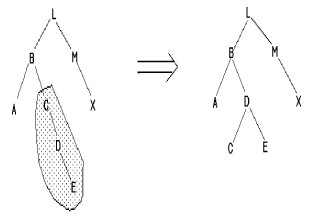
Insertion de D, E
 |
Insertion de H
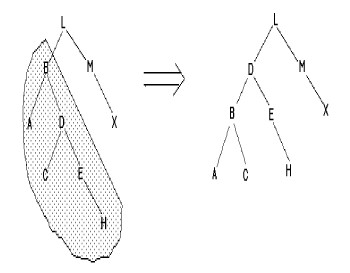 |
Insertion de R
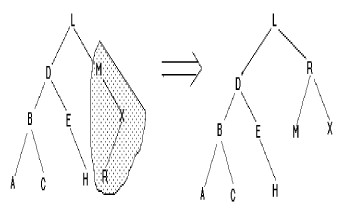 |
Insertion de F
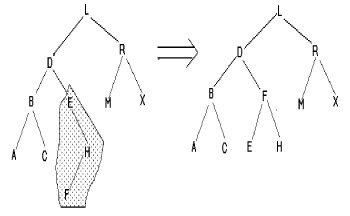 |
Définitions
Modèle
Opérations
Utilisation d'un arbre de recherche m-aires comme méthode d'accés
Implémentation
ISAM: Indexed Sequentiel Method (de IBM)
Un arbre de recherche m-aire peut être défini comme une généralisation de l'arbre de recherche binaire. Au lieu d'avoir une clé et deux pointeurs (cas d'un arbre de recherche binaire), on a (n-1)clés et n pointeurs. Un arbre de recherche m-aire d'ordre n est un arbre dans lequel chaque noeud peut avoir n fils.
![]() Si s1, s2, ... sn sont les n sous arbres issus d'un noeud donné
avec les clés k1, k2, ....,Kn-1 dans
l'ordre ascendant, alors :
Si s1, s2, ... sn sont les n sous arbres issus d'un noeud donné
avec les clés k1, k2, ....,Kn-1 dans
l'ordre ascendant, alors :
- toutes les clés dans s1 sont < k1
- toutes les clés dans sj (j=2,3, ...n-1) sont > kj-1 et < kj
- toutes les clés dans sn sont > kn-1.
La figure qui suit illustre un arbre de recherche m-aire d'ordre 4. les noeuds A, D, E et G contiennent le maximum de sous arbres : 4. On dit qu'ils sont remplis ou complets.
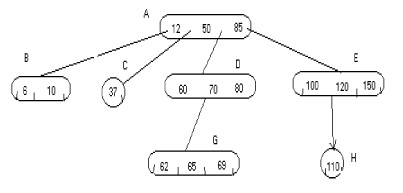 |
Un arbre de recherche m-aire "Top-Down" est tel que tout noeud non rempli est une feuille. L'arbre ci-dessus est "Top-Down" car les noeuds non remplis sont des feuilles.
![]() Un arbre de recherche m-aire est dit équilibré si tous ses feuilles sont au même niveau.
Un arbre de recherche m-aire est dit équilibré si tous ses feuilles sont au même niveau.
On peut définir les opérations suivantes sur les arbres de recherche m-aires :
| Nbr(P) : | accès au nombre de sous arbres du noeud P |
| Fils (P,1), Fils(P, 2), .....,Fils(P, Nbr(P)) : | accès aux différents fils. |
| Cle(P, 1), Clé(P,2), .......Clé(P, Nbr(P)-1) : | accès aux différentes clés |
| Aff_nbr(P, n) : | modifier le champ Nbr par la valeur n |
| Aff_fils(P, i, j) : | faire de j le i-ième fils du noeud P |
| Aff_Clé(P, i, clef) : | faire de clef la i-ième clé du noeud P |
| Allouer(P) : | allocation d'un noeud |
| Liberer(P) : | libération d'un noeud |
Le sous arbre pointé Par fils(P, i) contient toutes les clés entre Clé(P, i-1) et Clé(P,i).
Fils(P,1) Pointe le sous arbre des clés inférieures à Clé(P, 1).
Fils(P, Nbr(P)) pointe le sous arbre contenant toutes les clés supérieures à Clé(P,nbr(P)-1).
![]() Recherche
Recherche
L'algorithme de recherche est défini comme une généralisation de l'arbre de recherche binaire. Dans la figure suivante :
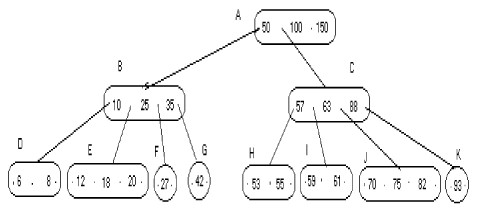 |
si nous recherchons les clés 63, 71, 22 et 41, nous obtenons les résultats suivants :
a) b) c) d) Clé=63 Clé=71 Clé=22 Clé=41 Noeud=C Noeud=J Noeud=E Noeud=G Position=2 Position=2 Position=4 Position=1 Trouv=Vrai Trouv=Faux Trouv=Faux Trouv=Faux
avec :
Clé : clé à rechercher.
Noeud : le noeud qui contient ou qui devrait contenir Clé.
Position : la position de la clé dans le noeud.
Trouv : existence de Clé.
![]() Insertion
Insertion
La construction est de haut en bas comme les arbres de recherche binaire et elle se fait en deux étapes . Rappelons que les clés dupliquées ne sont pas permises.
![]() Première étape : consiste à rechercher la
clé.
Première étape : consiste à rechercher la
clé.
![]() Deuxième
étape : Si la clé n'est pas trouvée, on est sur un noeud feuille, soit P.
Deuxième
étape : Si la clé n'est pas trouvée, on est sur un noeud feuille, soit P.
Si celui-ci n'est pas complet ( c'est à dire Nbr(P) < n) on l'insère.
Si celui-ci est complet, on fait les opérations suivantes :
- allocation d'un
nouveau noeud.
- insérer la clé(l'article)dans
ce noeud.
- placer le noeud comme
fils du noeud pointé par Noeud.
L'arbre ainsi construit dépend de l'ordre d'arrivée des clés. Il peut être très déséquilibré et donc beaucoup d'espace peut être perdu. Cette technique ne garantit donc pas l'équilibrage bien que l'arbre est "Top-Down", c'est à dire qu'un noeud n'est créé que si son noeud père est rempli.
![]() Suppression
Suppression
La suppression peut être logique ou physique.
Dans le premier cas, il suffit tout simplement de laisser la clé au niveau du noeud et la marquer. (implémentation : pointeur à l'article égal à NIL ou carrément utilisation d'un "flag"). La clé reste dans le noeud et est utilisée pour l'algorithme de recherche mais seulement elle ne représente pas une clé du fichier. Le grand inconvénient c'est quand il ya beaucoup de suppressions (un espace considérable est perdu ). Si une clé supprimée est réinsérée de nouveau, le même espace est réutilisé.
Dans le second cas, la technique est similaire à celle des arbres de recherche binaire, c'est à dire :
- si la clé a supprimer a un
sous arbre gauche ou droit vide, alors simplement supprimer la clé et tasser le noeud. Si
c'est la seule clé dans le noeud, libérer le noeud.
- si la clé à supprimer a des sous arbres gauche et droit tous les deux non vides, alors
trouver la clé successeur (qui doit avoir un sous arbre gauche vide). Remplacer la clé
à supprimer par ce successeur et tasser le noeud qui contenait ce successeur. Si le
successeur est la seule clé dans le noeud, libérer le noeud.
![]() Ces deux techniques ne garantissent pas le maintien de
l'arbre "Top-Down" même si avant la suppression ces qualités existaient. Il
faut donc trouver d'autres techniques pour préserver de telles qualités.
Ces deux techniques ne garantissent pas le maintien de
l'arbre "Top-Down" même si avant la suppression ces qualités existaient. Il
faut donc trouver d'autres techniques pour préserver de telles qualités.
![]() Parcours
Parcours
L'algorithme récursif suivant parcourt un arbre de recherche m-aire et liste les éléments dans l'ordre ascendant :
Traverse (Arbre) :
SI
Arbre <> NIL :
NT := Nbr(Arbre)
POUR I :=1, Nt-1
Traverse(Fils(Arbre, I))
ECRIRE(Clé(Arbre,I))
FINPOUR
Traverse(Fils(Arbre,Nt)
FSI
Utilisation d'un arbre de recherche m-aire comme méthode d'accès
L'arbre de recherche m-aire est surtout utilisé pour le stockage en mémoire externe(disque). Un noeud de l'arbre est alors une page sur le disque. A un moment donné, seule une page est ramenée en mémoire centrale. L'utilisation de ces sortes d'arbre pour le stockage nécessite des buffets de taille très grande( ordre de 200). Cette taille est cependant limitée par le système.
L'arbre de recherche m-aire est implementé par l'utilisation des fils explicites de chaque noeud au lieu de la représentation comme arbre binaire(liste de frères). La raison est que pour un tel arbre le nombre de fils est limité (ordre) et un noeud est toujours bien rempli.
Les articles peuvent
être rangés de deux façons :
(i) - dans les noeuds avec
les clés,
(ii) - séparément. On utilise alors un pointeur vers l'information. L'arbre de recherche
m-aire joue alors le rôle d'un index.
Si le fichier est grand on préfère de loin utiliser (ii) même si on fait une lecture supplémentaire pour retrouver l'article.
I S A M : Indexed Sequential Access Method (de IBM)
On peut définir le
séquentiel indexé comme suit :
a) pour localiser un article on utilise un index.
b) pour avoir le suivant, on ne repasse pas par
l'index.
Nous décrivons ci-après la méthode ISAM. Nous verrons plus loin une autre forme du séquentiel indexé.
ISAM utilise un arbre de recherche m-aire. De plus, ISAM est basée sur les
caractéristiques physiques du disque. Il existe 3 zones pour le fichier :
- une zone d'index,
- une zone de données,
- zone de débordements.
![]() Il y a 2 niveaux d'index :
Il y a 2 niveaux d'index :
- un index de cylindres
- des indexes de surfaces
![]() Structure du fichier
Structure du fichier
Le fichier est un ensemble de cylindres numérotés logiquement 1, 2, ... ,n. Le premier cylindre est réservé pour l'index. Les cylindres 2 à n-1 sont destinés aux données. Le cylindre n contiendra les débordements. Schématiquement, on a la figure suivante :
 |
![]() Structure d'un cylindre d'index
Structure d'un cylindre d'index
Le cylindre d'index est une table de couples ( Clei, Ci) avec Cléi, la plus grande clé dans le cylindre Ci.
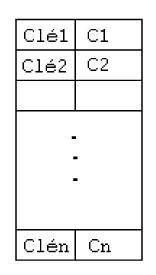 |
![]() Structure d'un cylindre de données
Structure d'un cylindre de données
Un cylindre de données
est un ensemble de surfaces divisé comme suit :
- une surface d'index,
- des surfaces de données,
- quelques surfaces pour les débordements du
cylindre.
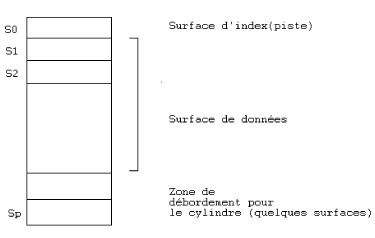 |
![]() Structure de la surface d'index
Structure de la surface d'index
Elle a la structure suivante :
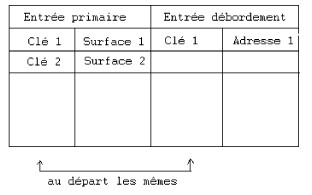 |
Pour les entrées
primaires, Cléi désigne la plus grande clé dans la surface surfacei. Pour les entrées
débordements, Cléi désigne la plus grande clé dans la liste des débordements.
Une adresse est le couple ( n? surface, n? article).
![]() Structure de la surface de données
Structure de la surface de données
C'est un tableau ordonné d'articles. Chaque article contient la clé et l'information.
 |
![]() Structure de la surface de débordements
Structure de la surface de débordements
 |
Les débordements sont
chaînés. Une adresse est composée de 3 champs :
- C : numéro de
cylindre
- S : numéro de
surface
- r : position de
l'article
![]() Structure du cylindre de débordements
Structure du cylindre de débordements
C'est un tableau de couples ( Art, Adr ). Art désigne l'article et Adr l'adresse du prochain article. Comme précédemment l'adresse est composée des trois champs C, S et r.
 |
![]() Opérations
Opérations
Chargement initial : |
cette opération consiste à créer le fichier à partir de données triées selon leur clé. Les surfaces de données ne sont pas remplies à 100 %. Les zones de débordements sont vides.
Recherche : |
une recherche d'article commence par la consultation de l'index des cylindres afin de sélectionner le cylindre de données. Ensuite la recherche continue au niveau de l'index des surfaces. Si la clé n'est pas dans son adresse primaire, la liste de débordements est consultée.
Insertion : |
si l'article n'existe pas, il peut être inséré :
a) dans une surface de données si la place est disponible,
b) dans la zone de débordements du même cylindre,
c) dans le cylindre de débordements.
| Suppression : |
la suppression est logique au niveau de l'article lui-même.
| Réorganisation : |
périodiquement, une réorganisation est nécessaire afin d'éliminer les débordements et pour récupérer les articles effacés logiquement.
Le problème avec les arbres de recherche m-aires est celui du maintien de l'équilibre de l'arbre paginé. Si l'ensemble des clés est connu à l'avance c'est simple. Le problème est compliqué si les clés arrivent de façon aléatoire. On peut garder les clés ordonnées à l'intérieur de la page(arbre AVL) mais il s'avère très dur de garder l'arbre de pages équilibré : l'équilibrage avec le maintien de l'ordre n'est pas évident. Essayer ....
Insérons la séquence de clés suivantes dans un arbre AVL paginé :
C S D T A M P I B W N G U R K E H O L J Y Q Z F X V
Nous obtenons l'arbre paginé suivant :
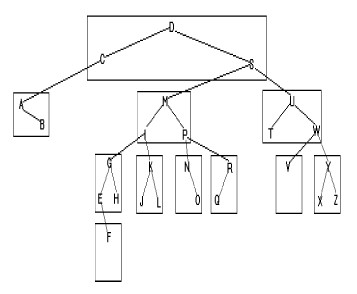 |
Problèmes :
1. Comment être sûr que les clés contenues dans la page racine sont dans leurs bonnes positions ?
2. comment garder l'arbre de pages équilibré ?
Bayer et McCreight ont fourni une solution à ces problèmes par l'invention des arbres B.
C'est une technique plus
complexe mais garantit l'équilibrage de l'arbre(donc recherche plus rapide). En plus,
chaque noeud de l'arbre(sauf la racine) est au moins rempli à moitié.(donc peu d'espace
perdu). C'est la raison pour laquelle elle est la plus utilisée dans les systèmes de
fichier actuels.
C'est donc une
construction Bottum-Up,
c'est à dire que l'arbre est construit de bas en haut. Par conséquent , l'équilibrage
est garanti.
Les éclatements peuvent être en cascade.
![]() Un arbre B d'ordre n est tel que :
Un arbre B d'ordre n est tel que :
- la racine a au moins 2 fils
- chaque noeud, qui n'est pas racine, a entre n/2 et n fils
- tous les noeuds feuilles sont au même niveau
Remarque : B pour Bayer / Boeng / Balanced
Dans ce qui suit, nous illustrons d'abord le mécanisme de construction d'un arbre B, ensuite nous donnons les techniques de la suppression à l'aide d'exemples.
Illustration du mécanisme d'insertion
Considérons l'arbre B suivant d'ordre 3 ( au maximum 2 clés et 3 pointeurs ) :
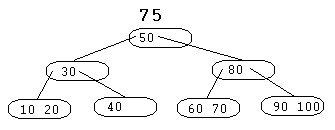 |
La clé 75 provoque l'éclatement du noeud (60 70). La clé du milieu, c'est à dire 70 est transférée dans le noeud père comme le montre la figure suivante :
|
La clé 55 est insérée dans le noeud contenant la clé 60. L'arbre devient :
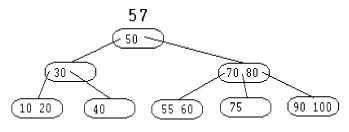 |
La clé 57 provoque une collision sur le noeud (55 60). Le noeud père (70 80) est à son tour éclaté. La clé 70 migre vers le noeud racine.
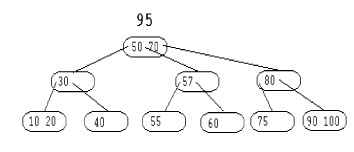 |
La clé 95 provoque l'éclatement du noeud (90 100). La clé 90 est donc déplacée dans le noeud contenant la clé 80 comme le montre la figure suivante :
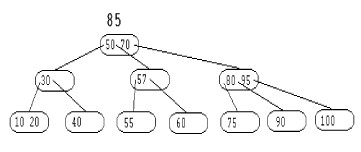 |
La clé 85 est insérée dans le noeud contenant la clé 90. L'arbre devient :
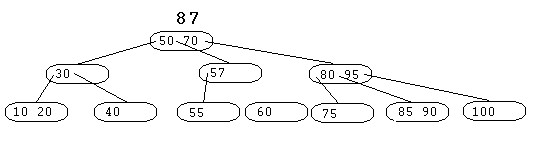 |
La clé 87 provoque une collision sur le noeud (85 90). Le noeud (80 95) est éclaté à son tour. Le noeud racine est aussi éclaté et le niveau de l'arbre augmente. On obtient ainsi l'arbre suivant :
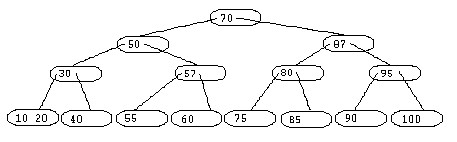 |
Techniques
de suppression
Il faut supprimer l'article tout en préservant la qualité de l'arbre B, c'est à dire en
gardant au moins
n div 2 clés dans le noeud.
C'est le cas de la suppression physique dans un arbre de recherche m-aire. En plus, si le noeud feuille qui contenait le successeur a moins de n div 2 clés l'action suivante est entreprise :
![]() Si l'un des frères(gauche ou droit) contient plus de n
div 2 clés, alors la clé, soit Ks, dans le noeud père qui sépare entre les deux
frères est ajoutée au noeud "underflow" et la dernière ou la première clé( première si frère droit,
dernière si frère gauche) est ajoutée au père à la place de Ks. La figure suivante
illustre le principe
Si l'un des frères(gauche ou droit) contient plus de n
div 2 clés, alors la clé, soit Ks, dans le noeud père qui sépare entre les deux
frères est ajoutée au noeud "underflow" et la dernière ou la première clé( première si frère droit,
dernière si frère gauche) est ajoutée au père à la place de Ks. La figure suivante
illustre le principe
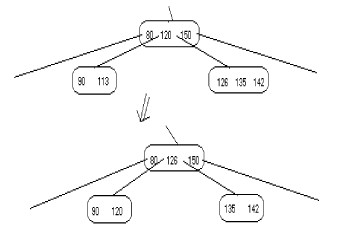 |
Suppression de la clé 113
![]() Si les deux frères contenaient
exactement n div 2 clés, le noeud "underflow" et l'un de ses frères seront concaténés ( fusionnés ou
consolidés) en un seul noeud qui contient aussi la clé séparatrice de leur père. La
figure suivante illustre le principe :
Si les deux frères contenaient
exactement n div 2 clés, le noeud "underflow" et l'un de ses frères seront concaténés ( fusionnés ou
consolidés) en un seul noeud qui contient aussi la clé séparatrice de leur père. La
figure suivante illustre le principe :
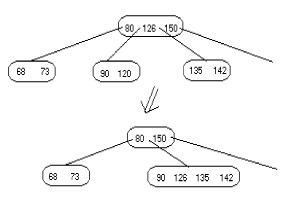 |
Suppression de la clé 120
et concaténation
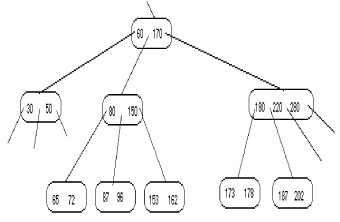
Il est aussi possible que le père contient seulement n div 2 clés et par conséquent il n'a pas de clé à donner. Dans ce cas, il peut emprunter de son père et frère comme dans la figure suivante :
 |
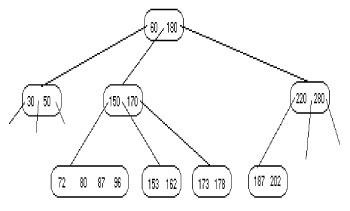 |
Suppression de 65, concaténation et emprunt
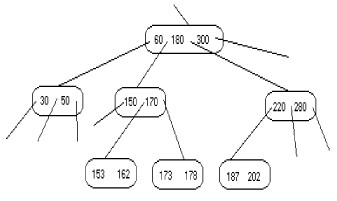
Dans le pire des cas, quand les frères du père n'ont pas de clés à donner, le père et son frère peuvent aussi être concaténés et une clé est prise du grand père. C'est le cas de la figure suivante :
 |
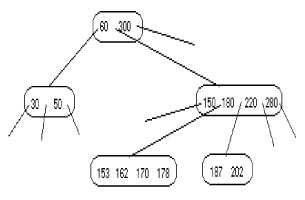 |
Suppression de 173
![]() Si tous les antécédents d'un noeud et leurs frères contiennent
exactement n div 2 clés, un clé sera prise de la racine (due aux concaténations en
cascades). Si la racine avait plus d'une clé, ceci termine le processus.
Si tous les antécédents d'un noeud et leurs frères contiennent
exactement n div 2 clés, un clé sera prise de la racine (due aux concaténations en
cascades). Si la racine avait plus d'une clé, ceci termine le processus.
![]() Si la racine contenait une seule clé, elle sera utilisée dans la
concaténation. Le noeud racine est libéré et le niveau de l'arbre est réduit d'une
unité.
Si la racine contenait une seule clé, elle sera utilisée dans la
concaténation. Le noeud racine est libéré et le niveau de l'arbre est réduit d'une
unité.
Une façon d'améliorer le chargement des arbres B consiste à retarder la division quand un noeud est plein. On fait alors une redistribution équitable des clés contenues dans le noeud en question et l'un de ses frères. Si le noeud et son frère sont tous les deux pleins, les deux noeuds sont divisés en 3. Ceci garantit un minimum de chargement à 67%. Un tel arbre B est appelé arbre B*.
Au lieu d'utiliser les clés intégralement on en utilise que des parties. C'est ce qu'on appelle des séparateurs. On ne peut utiliser la recherche binaire à cause de la longueur variable des séparateurs au niveau des noeuds. L'avantage des arbres B préfixés est que la profondeur diminue et donc l'accès est meilleur.
Dans un arbre B+ toutes les clés sont maintenues au niveau des feuilles. De plus, les clés sont dupliquées dans les noeuds non feuilles. Les articles(ou les pointeurs vers les articles) sont au niveau des feuilles. Les noeuds feuilles sont chaînés.
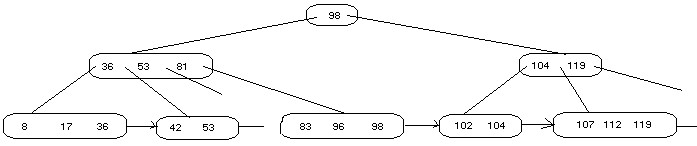 |
La liste liée des noeuds feuille est appelée ensemble des séquences.
La recherche ne s'arrête pas quand la clé est trouvée comme dans le cas des arbres B. La recherche se termine donc toujours au niveau d'un noeud feuille ( le signe < est remplacé par le signe <=).
C'est une généralisation du séquentiel indexé vu précédemment. Chaque niveau de l'arbre est un index au niveau suivant et le dernier niveau, l'ensemble des séquences, est un index au fichier lui-même.
L'insertion dans un arbre B+ est similaire à celle d'un arbre B sauf que le noeud de division est retenu dans le sous arbre gauche ( et bien sûr transféré dans le noeud père).
Quand une clé est supprimée, elle peut être retenue dans les noeuds non feuilles puisqu'elle reste un séparateur entre les clés dans les noeuds plus bas.
L'arbre B+ garde l'efficacité des opérations de recherche et d'insertion des arbres B mais améliore beaucoup l'efficacité de la recherche du suivant ( O(log(n) pour les arbres B et O(1) pour les arbres B+)
S I S : Scope Indexed Sequential (de CDC)
Nous décrivons, dans ce
qui suit, la méthode d'accès SIS dévéloppée par Control Data Corporation.
On a deux ensembles de bloc :
- un ensemble de blocs de données
- un ensemble de blocs d'index
Le bloc est l'unité de transfert entre la RAM et la mémoire secondaire.
Format d'un bloc de données
 |
L'espace libre est
toujours au milieu.
L'article est de longueur fixe ou variable. Si c'est variable, la clé est de longueur
fixe.
Format d'un
bloc d'index
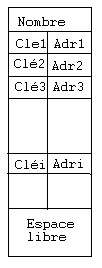 |
Les blocs de données et d'index sont organisés dans un arbre B+. Cléi désigne la plus petite valeur dans le bloc d'adresse Adri. Les blocs de données sont chaînés ( pour fournir l'accès séquentiel).L'expansion se fait par l'éclatement des noeuds.
Exemple
Montrons l'évolution de l'index et des blocs de données à partir d'un exemple.
Etat initial :
 |
Insertion de 105 :
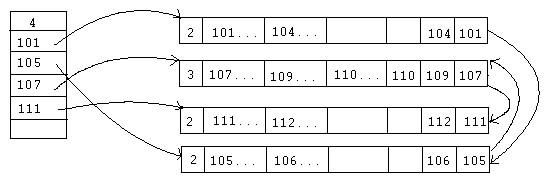 |
Il y a éclatement du bloc de données en deux.
Insertion de 108
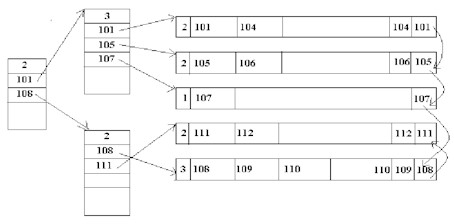 |
Il y a éclatement du
bloc en 2. De même, il y a éclatement du bloc d'index en 2.
Le fichier est dynamique , donc sans réorganisation future. On note ainsi l'absence des
débordements.
Les blocs de données et d'index ne sont pas nécessairement sur des positions contigu?.
Suppression de 107
 |
Le bloc de données contenant 107 est libéré. Il est rangé dans une liste linéaire chaînée de blocs libérés pour utilisation ultérieure.
Suppression de 101
Il faut mettre 104 à la place de 101 au niveau de l'index.
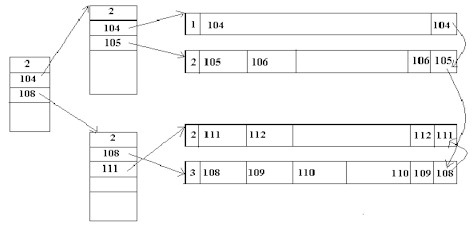 |
1. Retrouver les algorithmes de recherche,
insertion, suppression, requête à intervalle et de parcours en ordre croissant dans un
fichier structuré en arbre de recherche m-aire. On considère le cas o?les articles
sont rangés :
-avec les clés
- séparément
On examine le cas o?les articles sont de longueur :
-fixe
-variable
NB. Pour l'algorithme de recherche utiliser la fonction Rechnoeud (P, Clef) qui retourne soit le plus petit indice J tel que Clef <= Clé(P, J) ou Nbr(P) si clé est supérieur à toutes les clés dans Nœud(P).
Pour l'algorithme d'insertion on peut utiliser :
** La procédure Trouver qui a comme paramètre
En entrée : Arbre et Clef
En sortie
Si la clé est trouvée
Rech :pointe le nœud contenant la clé trouvée
Position :contient la position de la clé à l'intérieur du nœud.
Si la clé n'est pas trouvée
Rech : pointe la feuille qui pourrait contenir la clé.
Position : contient alors l'index de la plus petite clé dans le nœud pointé par Rech qui est supérieure à la clé recherchée Clef. Si toutes les clés dans le nœud pointé par Rech sont inférieures à Clef, Position est mis Nbr(Rech).
Une variable Trouv est mise à VRAI ou à FAUX selon l'appartenance ou non de la clé.
** La procédure Insérercle (Rech, Clef, Position) qui insère la clé Clef à la position Position dans le nœu Rech.
2. ISAM : Retrouver les algorithmes de recherche, insertion, suppression et de requête à intervalle pour la méthode d'accès ISAM présentée en cours.
3. Etudier et développer les algorithmes de recherche, insertion et de suppression dans un arbre AVL.
4. Retrouver les algorithmes de recherche, insertion et de suppression dans un fichier structuré en B-arbre.
5. SIS : Retrouver les algorithmes de recherche, insertion, suppression et de requête à intervalle pour la méthode d'accès SIS présentée en cours.