Sommaire Définition du langage d’expérimentation Compilateur pour le langage Z minimal Extensions du langage Z minimal
Chapitre précédent Chapitre 20 : Fonctions standards
20.1 Introduction
![]()
Le langage offre deux fonctions très utiles permettant de générer aléatoirement des chaînes de caractères (ALEACHAINE) et des entiers (ALEANOMBRE). Le langage offre aussi deux autres fonctions pour la manipulation des chaînes de caractères : CARACT et LONGCHAINE.
A la rencontre de ces opérations, l’analyseur sémantique les transforme en des formes internes qui permettent de faciliter leur interprétation ou génération de code. Il génère donc des quadruplets pour chaque opération rencontrée.
20.2 Quadruplets
![]()
Pour les fonctions ALEACHAINE(N) et ALEANOMBRE(N) les quadruplets suivants sont à générer:
- (‘Aleachaine’,A ,B, C )
A : pointeur dans TABOB vers l’entier N.
B : non utilisé.
C : pointeur dans TABOB vers le résultat de type entier .
- (‘Aléanombre’, A ,B, C )
A : pointeur dans TABOB vers l’entier N.
B : non utilisé.
C : pointeur dans TABOB vers le résultat de type chaîne de caractères.
Pour les fonctions sur les chaînes de caractères CARACT(Chaine, Rang) et LONGCHAINE(Chaine) les quadruplets suivants sont à générer:
- (‘Caract’,A ,B, C )
A : pointeur dans TABOB vers la chaîne de caractères.
B : pointeur dans TABOB vers le rang.
C : pointeur dans TABOB vers le résultat de type CHAINE.
- (‘Longchaine’, A ,B, C )
A : pointeur dans TABOB vers l’entier N.
B : non utilisé.
C : pointeur dans TABOB vers le résultat de type ENTIER.
20.3 Syntaxe
![]()
A ce niveau, notre grammaire devient complète avec l’intégration des fonctions standards en surbrillance.
Déclarations
<Algo Z> → [ ~Soit|Soient~ <Ps> ] Debut <Lis> Fin [;] { ~<Act> | <Fonct>~ [;] }*
<Act> → Action Idf [ ( <Li> ) ] [;] [ ~Soit|Soient~ <Ps> ] Debut <Lis> Fin
<Fonct> → Fonction Idf ( <Li> ) : <Typ> [ ~Soit|Soient~ <Ps> ] Debut <Lis> Fin
<Ps> → <S>;{ [~Soit|Soient~] <S>;}*
<S> → <Li> Sep ~<Typ>|~Action|Fonction(<Typ>)~ ~
<Li> → Idf {, Idf}*
<Typ> → Types | <Structsimple> | <Structcomplexe> |
Machine_car |
Machine_nombre |
[Pointeur vers [Sep] ] Liste
[ De ~Types | <Structsimple>~] |
Fichier De ~ Types | Vecteur(Cste) [De Types] | ~ <Structsimple> | <Structcomplexe> ~ ~
[Entete (Types {, Types }*)] Buffer <Li> |
Tableau (<Lc>) [De~<Structsimple> | Types~ ] |
<Structsimple> → [Structure ](Types {, Types }*)
<Structcomplexe> → [Structure ]( ~ Types | Vecteur(Cste)[De Types] ~ {, ~ Types | Vecteur(Cste) De [Types] ~ }*)
<Lc> → Cste {, Cste}*
Instructions
< Lis > → < Inst > { ; < Inst > }*
<Inst> → Idf := <Exp> |
Lire ( Idf {, Idf }* ) |
Ecrire (<Exp> {,<Exp>}* ) |
Tantque <Exp> [ : ] <Lis> Fintantque |
Si <Exp> [:] <Lis> [Sinon <Lis>] Fsi |
Pour Idf:= <Exp>,<Exp> [, <Exp>][:] <Lis> Finpour |
Appel Idf [(Exp {,<Exp>}*)]
~Liberer| Allouer | Fermer ~ ( <Exp> ) |
~ Aff_adr|Aff_val~ ( <Exp> , <Exp> ) |
Ouvrir ((Idf, Chaine, Chaine) |
~ Creer_liste |Init_vecteur|Init_struct|Creer_mnombre ~ ( Idf , [[ ~<Exp>|[[<Exp> {, <Exp>}*]] ~ {, ~<Exp>|[[<Exp> {, <Exp>}*]]~}* ]] ) |
Aff_element ( <Exp> [[ <Exp> {, <Exp> }* ]] ,<Exp> ) |
~ Aff_struct | Aff_entete ~ (Idf, Cste, <Exp>) |
Creer_mcar (Idf, [[ Chaine ]] )
~Lireseq|Ecrireseq|Rajouter|Lirecar|Lirenombre~(Idf, Idf) |
~ Liredir | Ecriredir ~ (Idf, <Exp>, Idf)
Expressions
<Exp> → <Exps>[ Opr <Exps>]
<Exps> → [Sign] <Terme> { Opa <Terme> }*
<Terme> → <Facteur>{Opm <Facteur>}*
<Facteur> → Idf [(Exp {,<Exp>}*)] | Cste | ( <Exp>) | <Fonct> | Nil | Non <Facteur> | Vrai | Faux | Chaine
<Fonct> → ~Valeur|Suivant~ ( <Fonct> ) |
Element ( <Fonct> [[ <Exp> {, <Exp> }* ]] ) |
~ Struct | Entete | ~ ( Idf, Cste) |
Caract ( Idf, <Exp>) |
~Nbrcar|Finfich|Alloc_bloc|NbrNombre ~ (Idf) |
~Aleachaine|Aleanombre|Longchaine~(<Exp>)
20.4 Fonctions sémantiques
![]()
Caract
<Fonct> → Caract ( Idf F1 , <Exp> ) F2
F1
Vérifier que Idf est une variable de type chaîne de caractères. Soit Ptidf son indice dans la table des objets TABOB.
F2
Soit Temp le résultat de <Exp>.
Vérifier que Temp est de type chaîne de caractères, sinon erreur. Soit Temp2 le temporaire crée pour contenir le résultat de la fonction.
Générer le quadruplet (‘Caract’, Ptidf, Temp, Temp2).
Aleachaine, Aleanombre et Longchaine
<Fonct> → ~ Aleachaine F1 |Aleanombre F1 | Longchaine F1 ~ (<Exp>) F2
F1
Sauv := Sem.
F2
Vérifier que le type de <Exp> correspond au type de la fonction. Soit Temp l’objet créé contenant le résultat de la fonction.
Générer le quadruplet (Sauv, , , Temp).
20.5 Exemple
![]()
La figure 39 montre les tables de compilation créées pour le programme source donné.
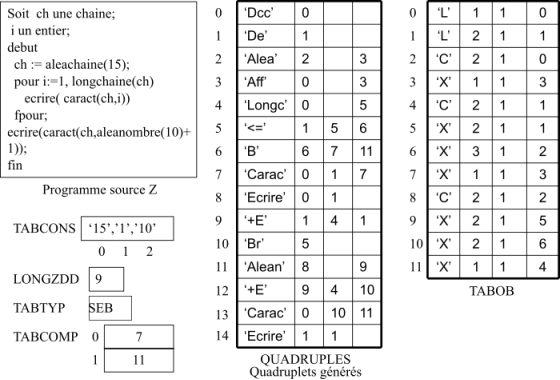
Figure 39: Tables de compilation(Fonctions standards)