Sommaire Définition du langage d’expérimentation Compilateur pour le langage Z minimal Extensions du langage Z minimal
Chapitre 11 : Expressions logiques Chapitre suivant
11.1 Introduction
![]()
Les expressions logiques sont traitées de la même façon que les expressions arithmétiques.
- OU est considéré comme + et –
- ET est considéré comme * et /
L’objectif de la sémantique des expressions logiques est de découper l’expression en opérations élémentaires. L’expression devient ainsi un programme. Il s’agit de générer les quadruplets propres aux expressions logiques au moyen de fonctions sémantiques insérées quelque part dans les règles syntaxiques.
Dans le but de faciliter la sémantique des expressions, aucune optimisation n’est considérée.
11.2 Quadruplets
![]()
- Pour les opérateurs binaires, nous considérons le quadruplet (Oper, B, C , D ).
Oper= Op || Type , Op dans {OU, ET } et Type = ‘B’ pour Booléen.
B, C : pointeurs dans TABOB vers les opérandes.
D : pointeur dans TABOB sur l’objet qui va contenir le résultat.
- Pour l’opérateur unaire le quadruplet (Oper, B, C , D ) est considéré.
Oper dans {NON}
B : pointeur dans TABOB vers l’opérande.
C : non utilisé.
D : pointeur dans TABOB sur l’objet qui va contenir le résultat.
11.3 Syntaxe
![]()
Rappelons ci-dessous la grammaire du langage Z minimal augmentée par les règles relatives aux expressions logiques en surbrillance.
<Algo Z> → [ ~Soit|Soient~ <Ps> ] Debut <Lis> Fin [;]
<Ps> → <S>;{ [~Soit|Soient~] <S>;}*
<S> → <Li> Sep <Typ>
<Li> → Idf {, Idf}*
<Typ> → Entier | Booleen
Instructions
< Lis > → < Inst > { ; < Inst > }*
<Inst> → Idf := <Exp> | Lire ( Idf {, Idf }* ) |Ecrire (<Exp> {,<Exp>}* )
Expressions
<Exp> → <Exps>[ Opr <Exps>]
<Exps> → [Sign] <Terme> { Opa <Terme> }*
<Terme> → <Facteur>{Opm <Facteur>}*
<Facteur> → Idf | Cste | ( <Exp>) | Non <Facteur> | Vrai | Faux
11.4 Fonctions sémantiques
![]()
Déclarations de booléens
Les fonctions sémantiques sont insérées dans le règles comme suit (en surbrillance) et sont décrites juste après.
<S> → <Li> Sep <Typ> F3
<Li> → Idf F2{, Idf F2}*
<Typ> → Entier | Booleen F1
F1
Récupérer le type dans Type.
F2
- Vérifier que l’identificateur Idf n’est pas déclaré (ne figure pas dans la table des symboles TABSYM), sinon Erreur.
- Sauvegarder l’identificateur Idf dans une liste L.
F3
Pour chaque Identificateur Idf déclaré comme BOOLEEN :
- Le mettre dans la table des symboles TABSYM.
- Lui attribuer une adresse relative et le mettre dans la table des objets TABOB (soit Pt son emplacement) avec le type ‘B’
- Générer le quadruplet (‘DB’, Pt, , )
Expressions logiques
Les fonctions sémantiques sont insérées dans le règles comme suit (en surbrillance) et sont décrites juste après.
<Exp> → <Exps>[ Opr <Exps> ]
<Exps> → <Terme> F6 { Opa F7 <Terme> F8 }*
<Terme> → <Facteur>{Opm F4 <Facteur> F5 }*
<Facteur> → Idf F1 | Cste | ( <Exp>) | Non <Facteur> F2 | Vrai F3 | Faux F3
F1
Vérifier que l’identificateur Idf est déclaré, sinon Erreur. Soit Pt1 son emplacement dans TABOB.
Retourner (Pt1).
F2
Générer une variable temporaire dans TABOB. Soit Ptx son emplacement dans TABOB.
Générer le quadruplet (‘Non’, Pt1, , Ptx).
Retourner (Ptx).
F3
Si la constante n’existe pas la mettre dans TABCONS et TABOB. Soit Pt1 son emplacement dans TABOB.
Retourner (Pt1).
F4
Sauvegarder l’opérateur dans une variable Op et le résultat de <Facteur> dans Temp1 (emplacement dans TABOB).
F5
Récupérer le résultat de <Facteur> dans Temp2 (emplacement dans TABOB).
Vérifier la compatibilité des types de Temp1 et Temp2.
Générer une variable temporaire. Soit Ptx son emplacement dans TABOB.
Générer le quadruplet (Op, Temp1, Temp2, Ptx).
Retourner (Ptx).
F6
Sauvegarder le résultat de <Terme> dans Temp1 (emplacement dans TABOB). Retourner (Temp1).
F7
Sauvegarder l’opérateur dans une variable Op.
F8
Récupérer le résultat de <Terme> dans Temp2 (emplacement dans TABOB).
Vérifier la compatibilité des types de Temp1 et Temp2.
Générer une variable temporaire. Soit Ptx son emplacement dans TABOB.
Générer le quadruplet (Op, Temp1, Temp2, Ptx).
Retourner (Ptx).
11.5 Exemple
La figure 14 montre les tables de compilation créées pour un programme source donné. Dans QUADRUPLES figure uniquement les quadruplets générés pour l’expression logique figurant dans l’opération d’écriture.
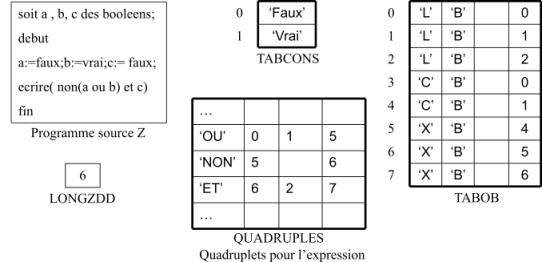
Figure 14: Tables de compilation (Expressions logiques)