Mécanisme de suppression

Étape 1 : comme dans un arbre de recherche binaire ordinaire

Étape 2 : remonter dans la pile, pour mettre à jour les balances ( processus en cascade)

Cas où la balance d’un nœud A devient +2

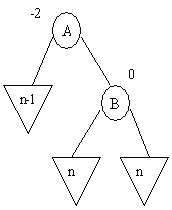
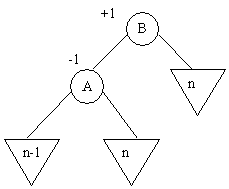
Le fils gauche B de A doit exister

Les cas suivants peuvent se présenter

a) B a une balance égale à + 1

Dans ce cas, on procède par une rotation droite autour de B

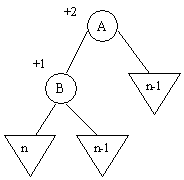
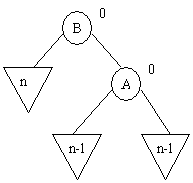
b) B a une balance égale à – 1

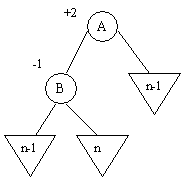
B a donc un fils à sa droite, soit C.

Dans ce cas, trois nouveaux cas peuvent se présenter

Pour les trois cas, on procède par une rotation gauche suivie par une rotation droite autour de C

b1) balance(C) = 0

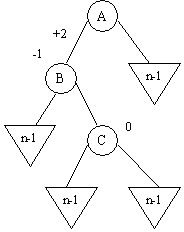
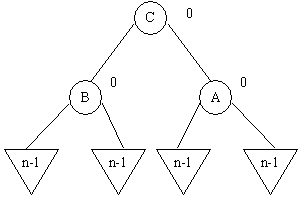
b2) balance(C) = +1

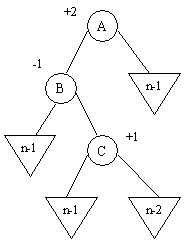
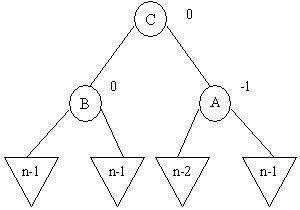
b2) Balance(C) = -1

 c) B a une balance égale à 0

On fait une rotation droite autour de B

Cas où la balance d’un nœud A devient –2

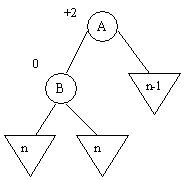
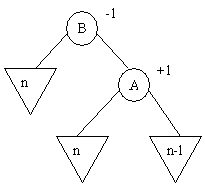
Le fils droit B de A doit exister

Les cas suivants peuvent se présenter

a) B a une balance égale à - 1

Dans ce cas procède par une rotation gauche autour de B

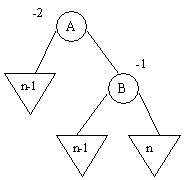
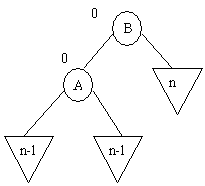
b) B a une balance égale à + 1

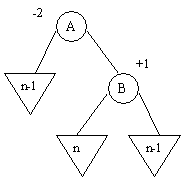
Dans ce cas, trois nouveaux cas peuvent se présenter

Rotation droite suivie par une rotation gauche autour de C

b1) Balance(c)=0

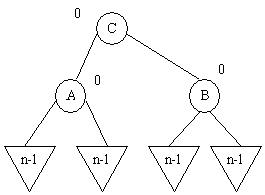
b1) Balance(c)=+1

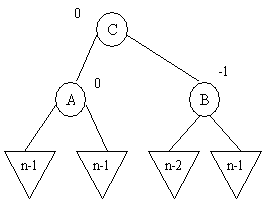
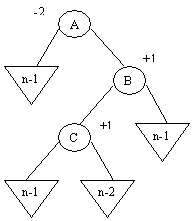
b1) Balance(c)=-1

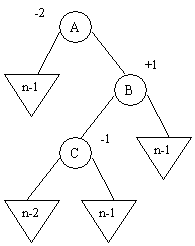
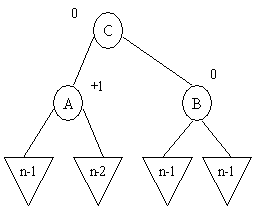
c)  

B a une balance égale à 0